

updated on 2019-08-18

損失関数の値をできるだけ小さくする最適なパラメータを見つけることを最適化
前章まで使ってきた最適化の手法は確率的勾配降下法(stochastic gradient descent)――略して SGD
式 $$W \leftarrow W - η \frac{ ∂L }{ ∂W } $$W←W−η∂L∂W
更新する重みパラメータを W、W に関する損失関数の勾配を ∂L / ∂W
ます。η は学習係数を表し、実際には 0.01 や 0.001 といった値を、前もって決めて使用
pythonでの実装
class SGD:
def __init__(self, lr=0.01):
self.lr = lr
def update(self, params, grads):
for key in params.keys():
params[key] -= self.lr * grads[key]lrは学習率params[key] は W1, W2などパラメータごとの値
grads[key] は W1, W2などパラメータごとの損失関数の微分
SGDの欠点は関数の形状が等方的でないとパラメータの更新が非効率
例えば、
式 $$f(x, y) = \frac{ 1 }{ 20 } x ^{ 2 } + y ^{ 2 } $$
という関数があったとすると、勾配はx軸方向が極端に小さくy軸方向に大きくなり、パラメータの更新経路がy軸方向にジグザグなり非効率な経路でパラメータを探索する。
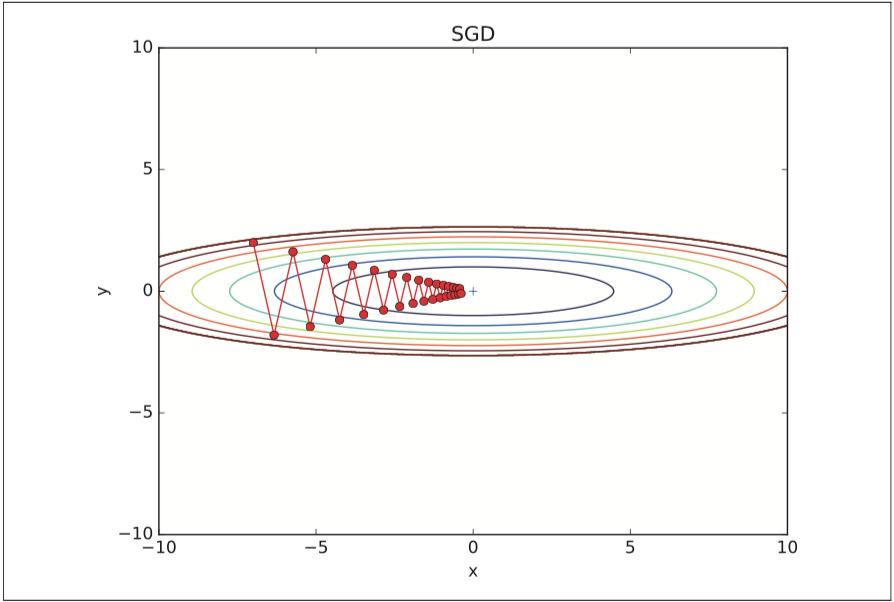
数式では以下のように表されます。
式
$$v \leftarrow αv - η\frac{ ∂L }{ ∂W } \\W \leftarrow W + v$$
W は更新する重みパラメータ、 ∂L/∂W は W に関する損失関の勾配、η は学習係数を表し、
v は物理で言うところの「速度」に対応し、α は物理で言うところの「空気抵抗」に対応。(物体が何も力を受けないときに徐々に減速するための役割)
筆者の考え方
慣性力がない( η(∂L/∂W)転がった時の勢いが残ってない) 考え方
・0<α<1 の時 Momentum
慣性力が残っている( η(∂L/∂W)転がった時の勢いが、空気抵抗で弱まってα(∂L/∂W) 残っている )
Momentum の実装(ソースコードは common/optimizer.py)
class Momentum: """Momentum SGD""" def __init__(self, lr=0.01, momentum=0.9): self.lr = lr self.momentum = momentum self.v = None def update(self, params, grads): # vが空のとき、params配列と同じ形状の0だけで埋められた配列を作る if self.v is None: self.v = {} for key, val in params.items(): self.v[key] = np.zeros_like(val) for key in params.keys(): self.v[key] = self.momentum*self.v[key] - self.lr*grads[key] params[key] += self.v[key]
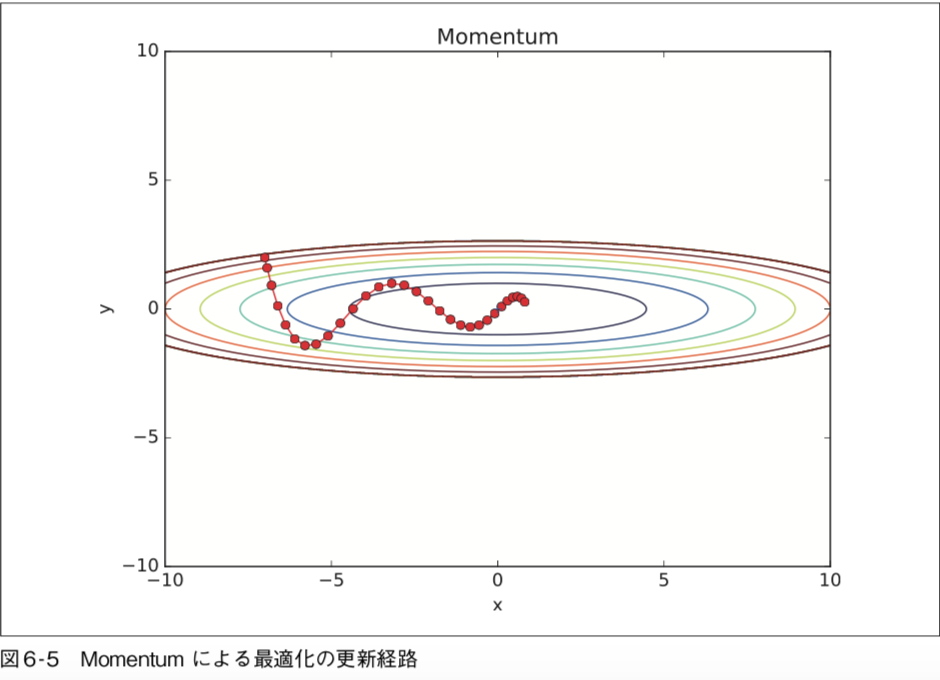
Momentumのイメージ: 更新経路はボールがお椀を転がるような動きをします。
ニューラルネットワークの学習係数では学習係数の値がかなり重要で、学習係数が小さすぎると学習に時間がかかりすぎてしまい、逆に大きすぎると発散して正しい学習が行えない。
そこで有効なのが学習係数を減衰させる方法。
このAdaGradは学習が進むにつれて学習係数ηを小さくする方法。
最初は“大きく”学習し、次第に“小さく”学習する
しかし無限に学習するとhがかなり大きくなりパラメータの更新が行われなくなってしまう。
数式
$$h \leftarrow h + \frac{ ∂L }{ ∂W } ⊙ \frac{ ∂L }{ ∂W } \\W \leftarrow W - η \dfrac{ 1 }{ \sqrt{ h } } \frac{ ∂L }{ ∂W } $$
(∂L/∂W) と 1/√h は反比例なので、パラメータが大きく更新されるほど学習率が小さくなり、更新量が大きな学習から小さな学習になっていく。
AdaGrad の実装(common/optimizer.py)
class AdaGrad:
"""AdaGrad"""
def __init__(self, lr=0.01):
self.lr = lr
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] += grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)1e-7を加算している意味は、分母が0になることを防ぐためです。
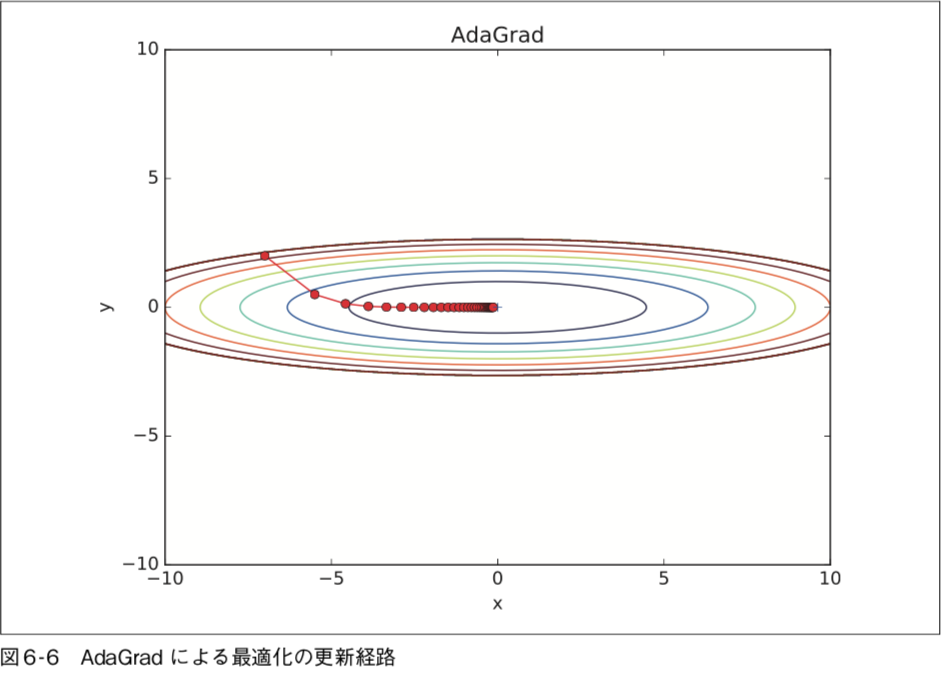
最小値に向かって効率的に動いているのが分かります。y 軸方向へは勾配が大きいため、最初は大きく動きますが、その大きな動きに比例し て、更新のステップが小さくなるように調整が行われます。そのため、y 軸方向への 更新度合いは弱められていき、ジグザグの動きが軽減されます。
AdaGradの無限に学習するとパラメータの更新が行われなくなるという問題を解決したのがRMSProp
勾配の2乗の指数移動平均をとるようにパラメータが更新されていく。つまり過去のAdaGradのようにすべての勾配を均一に加算するのではなく、新しい勾配の情報が大きく反映されるように加算する。
過去の勾配情報に0.9を何回も掛けたものを足しているので徐々に古いものの影響は小さくなる。
class RMSprop:
"""RMSprop"""
def __init__(self, lr=0.01, decay_rate = 0.99):
self.lr = lr
self.decay_rate = decay_rate
self.h = None
def update(self, params, grads):
if self.h is None:
self.h = {}
for key, val in params.items():
self.h[key] = np.zeros_like(val)
for key in params.keys():
self.h[key] *= self.decay_rate
self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)Momentum(お椀を転がる)とAdagrad(適応的に更新ステップを調整)の融合
もっともよく使われている最適化アルゴリズムである。
RMSprop の改良版であり,勾配に関しても以前の情報を指数的減衰させながら伝えることで,次元量の問題に対処している
式
$$初期値\ η=0.001,\beta _{ 1 }=0.9,\beta _{ 2 }=0.999,\ \epsilon= 10 ^{ -8 } \\m _{ t }=\beta _{ 1 }m_{ t-1 }\ + (1-\beta _{ 1 })g_{ t }\\v _{ t }=\beta _{ 2 }v_{ t-1 }\ + (1-\beta _{ 2 })g_{ t }^{ 2 } \\\hat{ {m _{ t }} }=\frac{ m _{ t } }{ 1-\beta _{ 1 }^{ t } } \\\hat{ {v _{ t }} }=\frac{ v _{ t } }{ 1-\beta _{ 2 }^{ t } } \\ \theta _{ t+1 }= \theta _{ t } - \dfrac{ η }{ \sqrt{ \hat{ {v _{ t }} } }+ \epsilon } \hat{ {m _{ t }} }\\ここで\hat{ {m _{ t }} },\hat{ {v _{ t }} }は勾配,二乗勾配の不偏推定量となるように調整したものである\\\beta _{ 1 }は一次モーメント用の係数, \beta _{ 2 }は二次モーメント用の係数$$
Adam の実装(common/optimizer.py)
class Adam: """Adam (http://arxiv.org/abs/1412.6980v8)""" def __init__(self, lr=0.001, beta1=0.9, beta2=0.999): self.lr = lr self.beta1 = beta1 self.beta2 = beta2 self.iter = 0 self.m = None self.v = None def update(self, params, grads): if self.m is None: self.m, self.v = {}, {} for key, val in params.items(): self.m[key] = np.zeros_like(val) self.v[key] = np.zeros_like(val) self.iter += 1 lr_t = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter) for key in params.keys(): #self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key] #self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2) self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key]) self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key]) params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7) #unbias_m += (1 - self.beta1) * (grads[key] - self.m[key]) # correct bias #unbisa_b += (1 - self.beta2) * (grads[key]*grads[key] - self.v[key]) # correct bias #params[key] += self.lr * unbias_m / (np.sqrt(unbisa_b) + 1e-7)
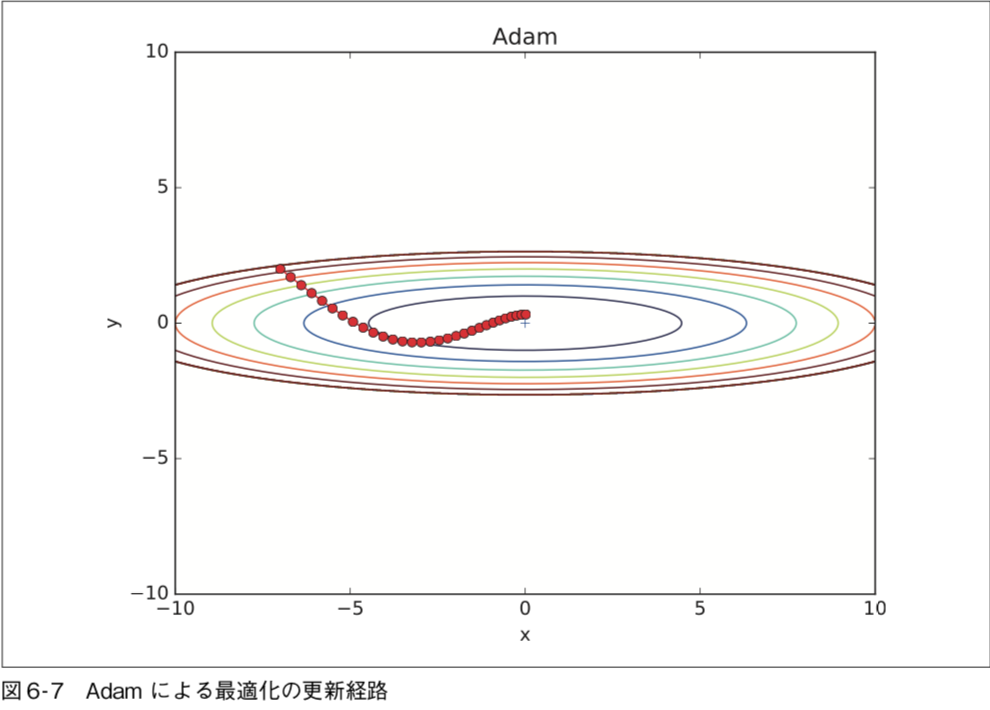
この図だけを見ると AdaGrad が一番良さそうですが、これは解くべき問題に よって結果が変わるので注意が必要である。
ハイパーパ ラメータ(学習係数など)の設定値によっても結果が変わる
4 つの手法―― SGD、Momentum、 AdaGrad、Adam――の経路を比較
(ソースコードは ch06/optimizer_compare_naive.py)
import sys, os sys.path.append(os.pardir) # 親ディレクトリのファイルをインポートするための設定 import numpy as np import matplotlib.pyplot as plt from collections import OrderedDict from common.optimizer import * def f(x, y): return x**2 / 20.0 + y**2 def df(x, y): return x / 10.0, 2.0*y init_pos = (-7.0, 2.0) params = {} params['x'], params['y'] = init_pos[0], init_pos[1] grads = {} grads['x'], grads['y'] = 0, 0 optimizers = OrderedDict() optimizers["SGD"] = SGD(lr=0.95) optimizers["Momentum"] = Momentum(lr=0.1) optimizers["AdaGrad"] = AdaGrad(lr=1.5) optimizers["Adam"] = Adam(lr=0.3) idx = 1 for key in optimizers: optimizer = optimizers[key] x_history = [] y_history = [] params['x'], params['y'] = init_pos[0], init_pos[1] for i in range(30): x_history.append(params['x']) y_history.append(params['y']) grads['x'], grads['y'] = df(params['x'], params['y']) optimizer.update(params, grads) x = np.arange(-10, 10, 0.01) y = np.arange(-5, 5, 0.01) X, Y = np.meshgrid(x, y) Z = f(X, Y) # for simple contour line mask = Z > 7 Z[mask] = 0 # plot plt.subplot(2, 2, idx) idx += 1 plt.plot(x_history, y_history, 'o-', color="red") plt.contour(X, Y, Z) plt.ylim(-10, 10) plt.xlim(-10, 10) plt.plot(0, 0, '+') #colorbar() #spring() plt.title(key) plt.xlabel("x") plt.ylabel("y") plt.show()
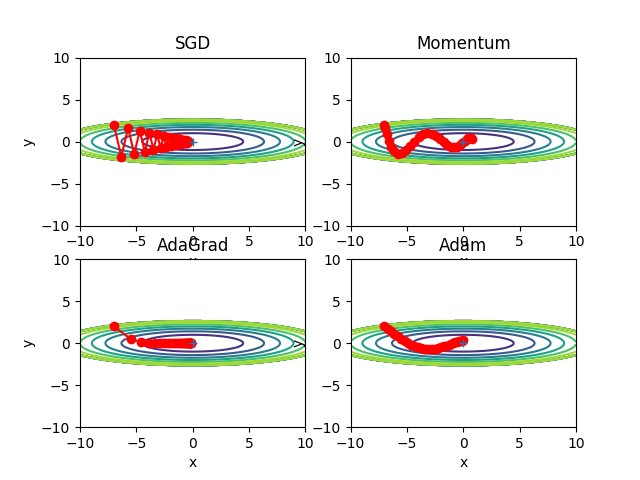
学習の進み具合を比べる
(ソースコードは ch06/optimizer_compare_mnist.py)
import os import sys sys.path.append(os.pardir) # 親ディレクトリのファイルをインポートするための設定 import matplotlib.pyplot as plt from dataset.mnist import load_mnist from common.util import smooth_curve from common.multi_layer_net import MultiLayerNet from common.optimizer import * # 0:MNISTデータの読み込み========== (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True) train_size = x_train.shape[0] batch_size = 128 max_iterations = 2000 # 1:実験の設定========== optimizers = {} optimizers['SGD'] = SGD() optimizers['Momentum'] = Momentum() optimizers['AdaGrad'] = AdaGrad() optimizers['Adam'] = Adam() #optimizers['RMSprop'] = RMSprop() networks = {} train_loss = {} for key in optimizers.keys(): networks[key] = MultiLayerNet( input_size=784, hidden_size_list=[100, 100, 100, 100], output_size=10) train_loss[key] = [] # 2:訓練の開始========== for i in range(max_iterations): batch_mask = np.random.choice(train_size, batch_size) x_batch = x_train[batch_mask] t_batch = t_train[batch_mask] for key in optimizers.keys(): grads = networks[key].gradient(x_batch, t_batch) optimizers[key].update(networks[key].params, grads) loss = networks[key].loss(x_batch, t_batch) train_loss[key].append(loss) if i % 100 == 0: print( "===========" + "iteration:" + str(i) + "===========") for key in optimizers.keys(): loss = networks[key].loss(x_batch, t_batch) print(key + ":" + str(loss)) # 3.グラフの描画========== markers = {"SGD": "o", "Momentum": "x", "AdaGrad": "s", "Adam": "D"} x = np.arange(max_iterations) for key in optimizers.keys(): plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key) plt.xlabel("iterations") plt.ylabel("loss") plt.ylim(0, 1) plt.legend() plt.show()
5 層のニューラルネットワーク、各層100 個のニューロンを持つネットワーク、活性化関数はReLU を使用
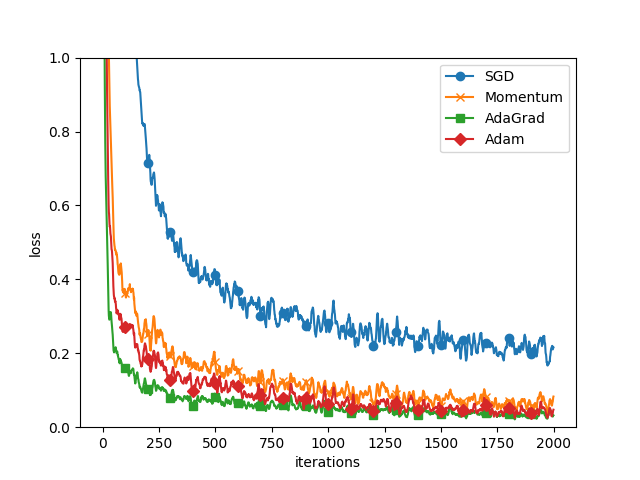
上図より、SGD よりも他の手法が速く学習できていることが分かる。
中でも、 AdaGrad の学習が少しだけ速く行われている。
実験の注意点: 学習係数のハイパーパラメータや、ニューラルネットワークの構造(何層の深さ か、など)によって結果は変化する。
ただし、一般に SGD よりも他 の 3 つの手法のほうが速く学習でき、時には最終的な認識性能も高くなる。
重みの初期値の設定で学習の成否が別れることは実際によくある。
推奨される重みの初期値について説明し、実験によって実際にニューラルネットワークの学習が速やかに行われることを確認する。
誤差逆伝播法によって、全ての重みの値が均一に更新されてしまい、たくさんの重みを持つ意味がなくなってしまう。
ここでは対称性を破ることが不可欠であり、パフォーマンスの理由ではありません。
多層パーセプトロン(入力層と隠れ層)の最初の2つの層を想像してください。
順方向伝搬中、隠れ層のユニットは、入力の合計に対応する重みを掛け合わせます。
今度は、すべての重みを同じ値(0または1など)に初期化するとします。この場合、各隠れユニットは全く同じ信号を得るでしょう。
すべての重みが1に初期化されると、各ユニットは全て、入力の合計に等しい信号を得る(xの総和)。
すべての重みがゼロである場合、それはさらに悪化し、すべての隠れ層のユニットはゼロ信号を得る。
入力が何であっても、すべての重みが同じであれば、隠れ層のすべてのユニットも同じになります。
重みの対称的な構造を崩す――ために、ランダムな初期値が必要なのです。
Weight decay:重みパラメータの値を小さくするように学習を行うことを目的とした手法。
重みの値を小さくすることで、過学習が起きにくくなる。
実際、これまでの重みの初期値、0.01 * np.random.randn(10, 100)だった。
(標準偏差が0.01のガウス分布)
結論を先に述べると以下になる
前層のノードの個数がnの際に
$$Xavierの初期値:標準偏差が \dfrac{ 1 }{ \sqrt{ n } } の標準偏差を持つガウス分布$$
$$Heの初期値:標準偏差が\dfrac{ 2 }{ \sqrt{ n } }の標準偏差を持つガウス分布$$
重みの初期値によって隠れ層のアクティベーションがどのように変化するかを調べる。
5 つの層があり、それぞれの層は 100 個のニューロンを持つものとする(活性化関数にシグモイド関数を使用)
(ch06/weight_init_activation_ histogram.py)
import numpy as np import matplotlib.pyplot as plt def sigmoid(x): return 1 / (1 + np.exp(-x)) def ReLU(x): return np.maximum(0, x) def tanh(x): return np.tanh(x) input_data = np.random.randn(1000, 100) # 1000個のデータ node_num = 100 # 各隠れ層のノード(ニューロン)の数 hidden_layer_size = 5 # 隠れ層が5層 activations = {} # ここにアクティベーション(活性化関数の後の出力データ)の結果を格納する x = input_data for i in range(hidden_layer_size): if i != 0: x = activations[i-1] # 初期値の値をいろいろ変えて実験しよう! w = np.random.randn(node_num, node_num) * 1 # w = np.random.randn(node_num, node_num) * 0.01 # w = np.random.randn(node_num, node_num) * np.sqrt(1.0 / node_num) # w = np.random.randn(node_num, node_num) * np.sqrt(2.0 / node_num) a = np.dot(x, w) # 活性化関数の種類も変えて実験しよう! z = sigmoid(a) # z = ReLU(a) # z = tanh(a) activations[i] = z # ヒストグラムを描画 for i, a in activations.items(): plt.subplot(1, len(activations), i+1) plt.title(str(i+1) + "-layer") if i != 0: plt.yticks([], []) # plt.xlim(0.1, 1) # plt.ylim(0, 7000) plt.hist(a.flatten(), 30, range=(0,1)) plt.show()
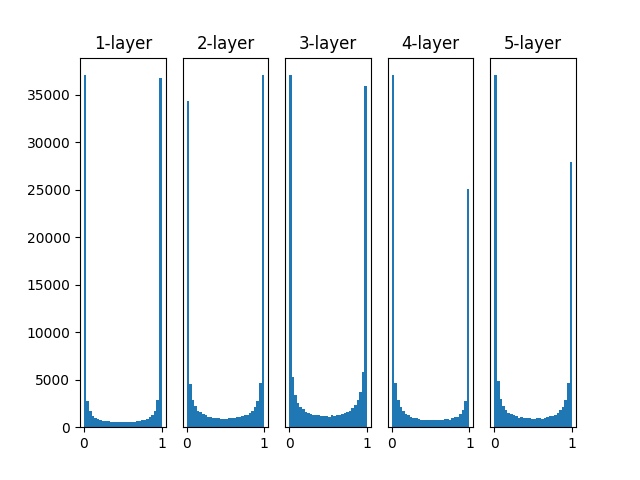 重みの初期値として標準偏差 1 のガウス分布を用いたときの、各層のアクティベーション の分布
重みの初期値として標準偏差 1 のガウス分布を用いたときの、各層のアクティベーション の分布
各層のアクティベーションは 0 と 1 に偏った分布になっている。
-> 0 と 1 に偏ったデータ分布では、逆伝播 での勾配の値がどんどん小さくなって消えてしまう。
勾配消失(gradient vanishing)が起きる
# w = np.random.randn(node_num, node_num) * 1 w = np.random.randn(node_num, node_num) * 0.01
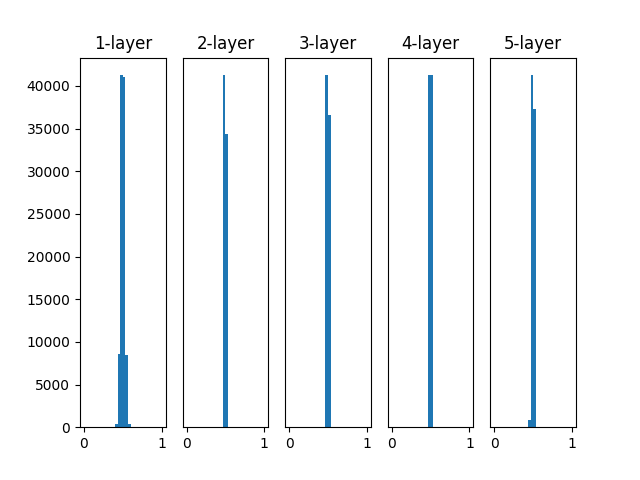
各層のアクティベーションは0.5付近に集中する分布になっている。
0と1の偏りがないため、勾配消失の問題が起きないが...
アクティベーションに偏りがある
-> ほとんど同じ値を出力するとすれば、複数のニューロンが存在する意味がなくなってしまう。
「表現力が制限される」
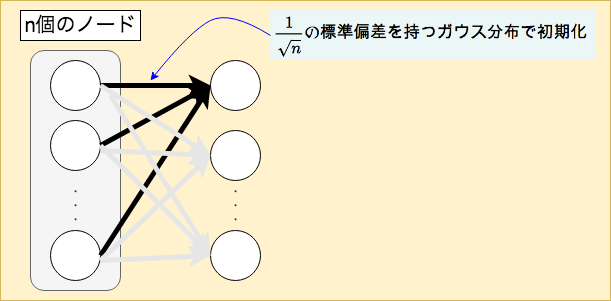
node_num = 100 # 前層のノードの数 w = np.random.randn(node_num, node_num) / np.sqrt(node_num)
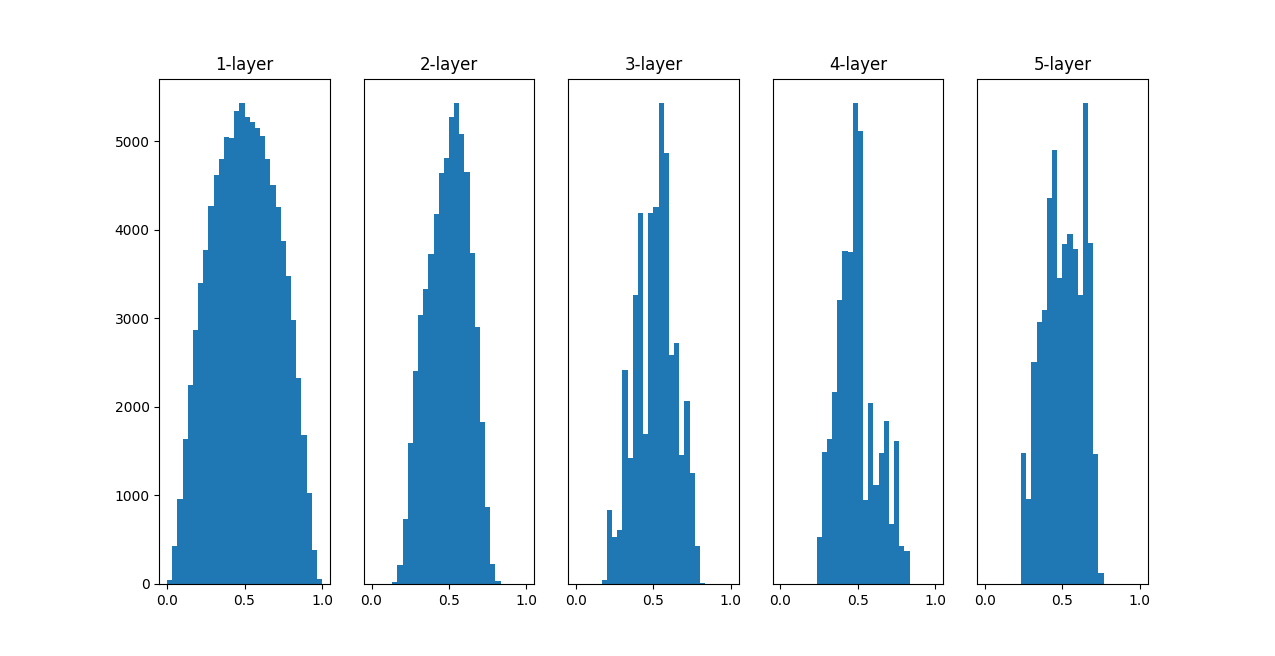
これまでよりも、広がりを持った分布になる
-> 効率的に学習が行える
「Xavier の初期値」は、活性化関数が線形であることを前提に導いた結果。
sigmoid 関数や tanh 関数は左右対称で中央付近が線形関数として見なせるので、 「Xavier の初期値」が適している。
一方、ReLU を用いる場合は、ReLU に特化した初期値を用いることが推奨されている。
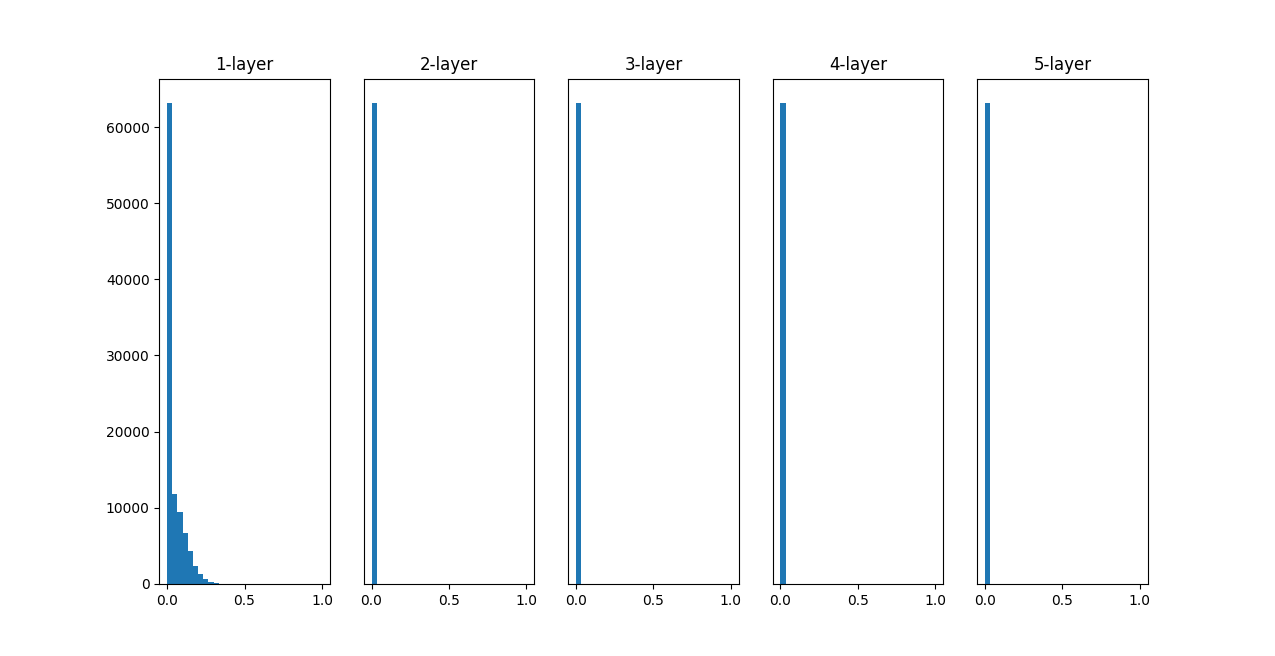 標準偏差が0.01のガウス分布を重みの初期値とした場合
標準偏差が0.01のガウス分布を重みの初期値とした場合
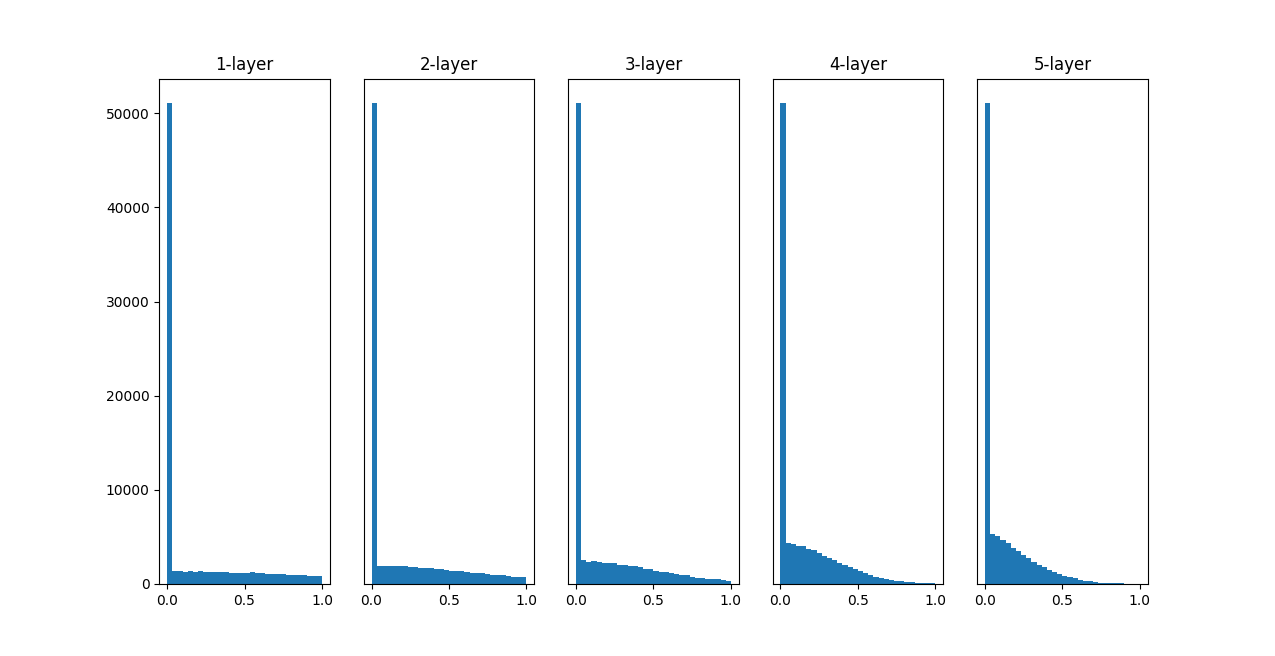 「Xavierの初期値」の場合
「Xavierの初期値」の場合
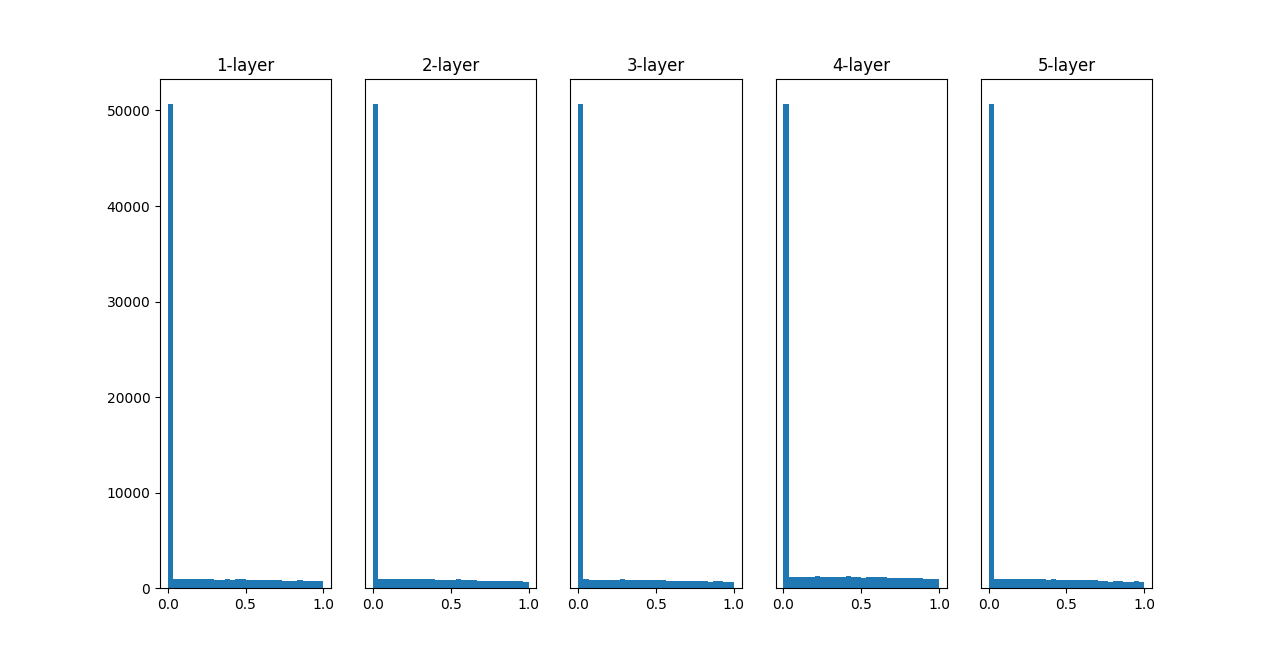 「Heの初期値」の場合
「Heの初期値」の場合
重みの初期値の与え方の違いによって、ニューラルネッ トワークの学習にどれだけ影響を与えるか見てみる
(ch06/wight_init_compare.py)
# coding: utf-8
import os
import sys
sys.path.append(os.pardir) # 親ディレクトリのファイルをインポートするための設定
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.util import smooth_curve
from common.multi_layer_net import MultiLayerNet
from common.optimizer import SGD
# 0:MNISTデータの読み込み==========
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
train_size = x_train.shape[0]
batch_size = 128
max_iterations = 2000
# 1:実験の設定==========
weight_init_types = {'std=0.01': 0.01, 'Xavier': 'sigmoid', 'He': 'relu'}
optimizer = SGD(lr=0.01)
networks = {}
train_loss = {}
for key, weight_type in weight_init_types.items():
networks[key] = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100],
output_size=10, weight_init_std=weight_type)
train_loss[key] = []
# 2:訓練の開始==========
for i in range(max_iterations):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
for key in weight_init_types.keys():
grads = networks[key].gradient(x_batch, t_batch)
optimizer.update(networks[key].params, grads)
loss = networks[key].loss(x_batch, t_batch)
train_loss[key].append(loss)
if i % 100 == 0:
print("===========" + "iteration:" + str(i) + "===========")
for key in weight_init_types.keys():
loss = networks[key].loss(x_batch, t_batch)
print(key + ":" + str(loss))
# 3.グラフの描画==========
markers = {'std=0.01': 'o', 'Xavier': 's', 'He': 'D'}
x = np.arange(max_iterations)
for key in weight_init_types.keys():
plt.plot(x, smooth_curve(train_loss[key]), marker=markers[key], markevery=100, label=key)
plt.xlabel("iterations")
plt.ylabel("loss")
plt.ylim(0, 2.5)
plt.legend()
plt.show()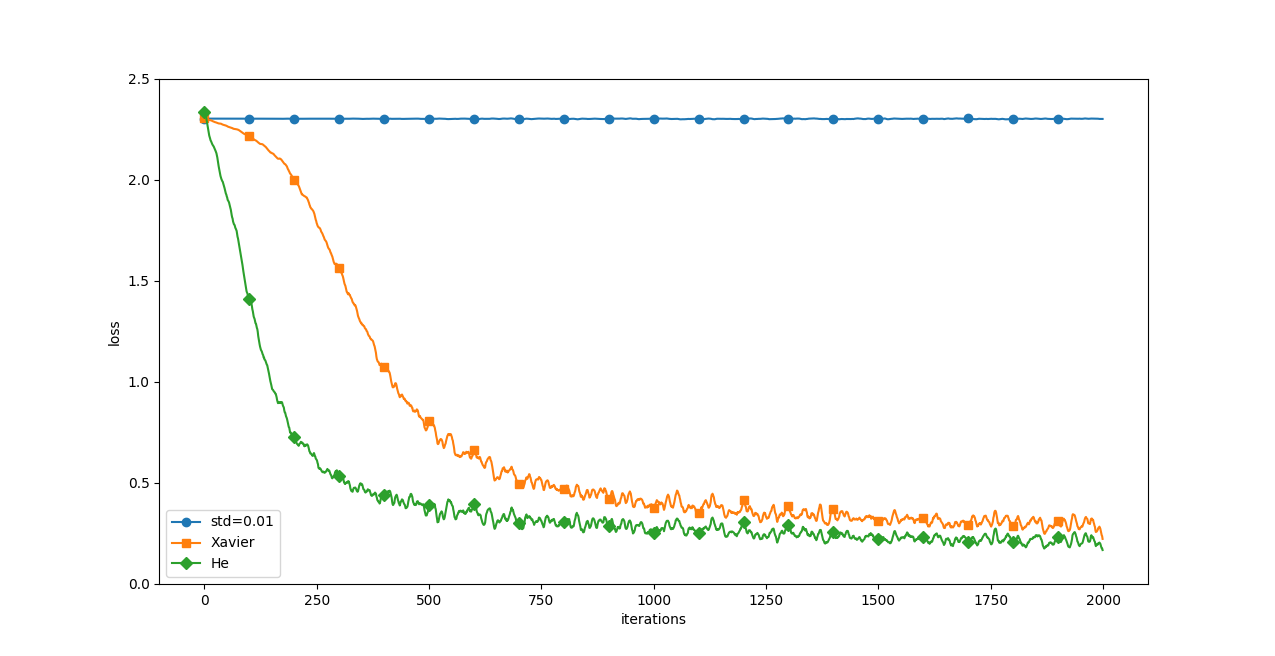 MNIST テータセットに対する「重みの初期値」による比較:横軸は学習の繰り返し回数 (iterations)、縦軸は損失関数の値(loss)
MNIST テータセットに対する「重みの初期値」による比較:横軸は学習の繰り返し回数 (iterations)、縦軸は損失関数の値(loss)
5 層のニューラルネットワーク(各層 100 個のニューロン)で、活性化関数として ReLU を使用
「std=0.01」の場合はほとんど学習が進んでいおらず
He、Xavierの際にはサクサク学習が進んでいる
そして、「He の初期値」のほうが、学習の進みが速い
→初期値の問題はとても重要ということがわかる
各層のアクティベーションの分布が適度な広がりを持つように”強制的”にアクティベーションの調整を行う
Batch Normalizationの利点
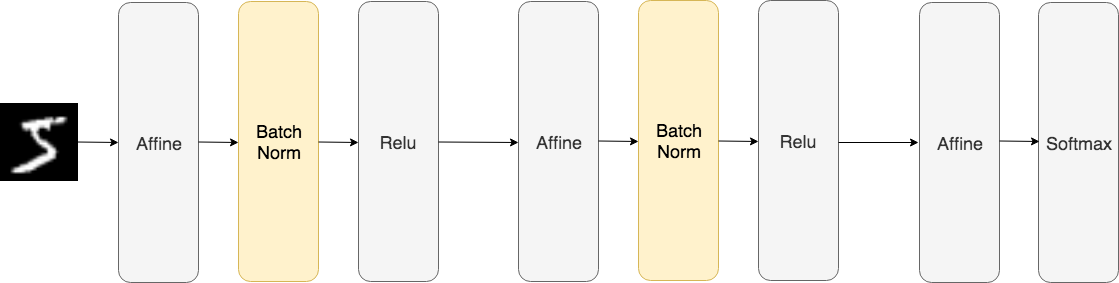 Batch Normalization を使用したニューラルネットワークの例(Batch Norm レイヤは背景 をオレンジで描画)
Batch Normalization を使用したニューラルネットワークの例(Batch Norm レイヤは背景 をオレンジで描画)
さらにBath Normレイヤは、この正規化されたデータに対して、固有のスケールとシフトで変換を行います。
γ、βはパラメータで、最初はγ=1、β=0からスタートして、学習によって適した値に調整されていきます。
Batch Norm レイヤを使って、実験する。
ソースコードは、ch06/batch_norm_test.py)
import sys, os
sys.path.append(os.pardir) # 親ディレクトリのファイルをインポートするための設定
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.multi_layer_net_extend import MultiLayerNetExtend
from common.optimizer import SGD, Adam
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
# 学習データを削減
x_train = x_train[:1000]
t_train = t_train[:1000]
max_epochs = 20
train_size = x_train.shape[0]
batch_size = 100
learning_rate = 0.01
def __train(weight_init_std):
bn_network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100], output_size=10,
weight_init_std=weight_init_std, use_batchnorm=True)
network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100], output_size=10,
weight_init_std=weight_init_std)
optimizer = SGD(lr=learning_rate)
train_acc_list = []
bn_train_acc_list = []
iter_per_epoch = max(train_size / batch_size, 1)
epoch_cnt = 0
for i in range(1000000000):
batch_mask = np.random.choice(train_size, batch_size)
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
for _network in (bn_network, network):
grads = _network.gradient(x_batch, t_batch)
optimizer.update(_network.params, grads)
if i % iter_per_epoch == 0:
train_acc = network.accuracy(x_train, t_train)
bn_train_acc = bn_network.accuracy(x_train, t_train)
train_acc_list.append(train_acc)
bn_train_acc_list.append(bn_train_acc)
print("epoch:" + str(epoch_cnt) + " | " + str(train_acc) + " - " + str(bn_train_acc))
epoch_cnt += 1
if epoch_cnt >= max_epochs:
break
return train_acc_list, bn_train_acc_list
# 3.グラフの描画==========
weight_scale_list = np.logspace(0, -4, num=16)
x = np.arange(max_epochs)
for i, w in enumerate(weight_scale_list):
print( "============== " + str(i+1) + "/16" + " ==============")
train_acc_list, bn_train_acc_list = __train(w)
plt.subplot(4,4,i+1)
plt.title("W:" + str(w))
if i == 15:
plt.plot(x, bn_train_acc_list, label='Batch Normalization', markevery=2)
plt.plot(x, train_acc_list, linestyle = "--", label='Normal(without BatchNorm)', markevery=2)
else:
plt.plot(x, bn_train_acc_list, markevery=2)
plt.plot(x, train_acc_list, linestyle="--", markevery=2)
plt.ylim(0, 1.0)
if i % 4:
plt.yticks([])
else:
plt.ylabel("accuracy")
if i < 12:
plt.xticks([])
else:
plt.xlabel("epochs")
plt.legend(loc='lower right')
plt.show()重みの初期値の標準偏差をさまざまな値に変えたときの学習経過のグラフを描画。
ほとんどすべてのケースで、Batch Norm を使用したほうが学習の進みが速い。
Batch Norm を用いない場合は、良い初期値のスケールを与えないと、まったく学習が進まない。
Batch Norm を使用することで、学習の進行を促進させる ことができ、また、重みの初期値にロバストになります(「初期値にロバスト」とは、 初期値にそれほど依存しない、ということを表します)
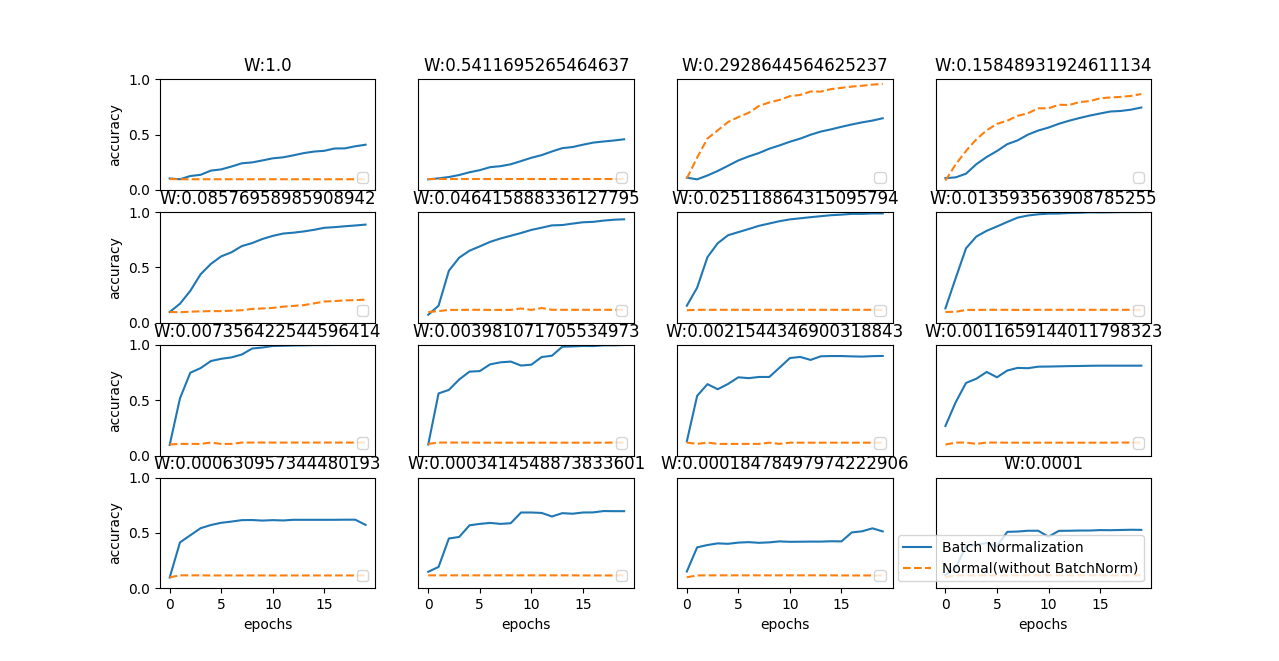 グラフの実線が Batch Norm を使用した場合の結果、点線が Batch Norm を使用しなかった 場合の結果:図のタイトルに重みの初期値の標準偏差を表記する
グラフの実線が Batch Norm を使用した場合の結果、点線が Batch Norm を使用しなかった 場合の結果:図のタイトルに重みの初期値の標準偏差を表記する
過学習が起きる原因
過学習をわざと発生させる(該当ファイルは ch06/overfit_weight_ decay.py)
import os import sys sys.path.append(os.pardir) # 親ディレクトリのファイルをインポートするための設定 import numpy as np import matplotlib.pyplot as plt from dataset.mnist import load_mnist from common.multi_layer_net import MultiLayerNet from common.optimizer import SGD (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True) # 過学習を再現するために、学習データを削減 x_train = x_train[:300] t_train = t_train[:300] # weight decay(荷重減衰)の設定 ======================= weight_decay_lambda = 0 # weight decayを使用しない場合 #weight_decay_lambda = 0.1 # ==================================================== network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10, weight_decay_lambda=weight_decay_lambda) optimizer = SGD(lr=0.01) max_epochs = 201 train_size = x_train.shape[0] batch_size = 100 train_loss_list = [] train_acc_list = [] test_acc_list = [] iter_per_epoch = max(train_size / batch_size, 1) epoch_cnt = 0 for i in range(1000000000): batch_mask = np.random.choice(train_size, batch_size) x_batch = x_train[batch_mask] t_batch = t_train[batch_mask] grads = network.gradient(x_batch, t_batch) optimizer.update(network.params, grads) if i % iter_per_epoch == 0: train_acc = network.accuracy(x_train, t_train) test_acc = network.accuracy(x_test, t_test) train_acc_list.append(train_acc) test_acc_list.append(test_acc) print("epoch:" + str(epoch_cnt) + ", train acc:" + str(train_acc) + ", test acc:" + str(test_acc)) epoch_cnt += 1 if epoch_cnt >= max_epochs: break # 3.グラフの描画========== markers = {'train': 'o', 'test': 's'} x = np.arange(max_epochs) plt.plot(x, train_acc_list, marker='o', label='train', markevery=10) plt.plot(x, test_acc_list, marker='s', label='test', markevery=10) plt.xlabel("epochs") plt.ylabel("accuracy") plt.ylim(0, 1.0) plt.legend(loc='lower right') plt.show()
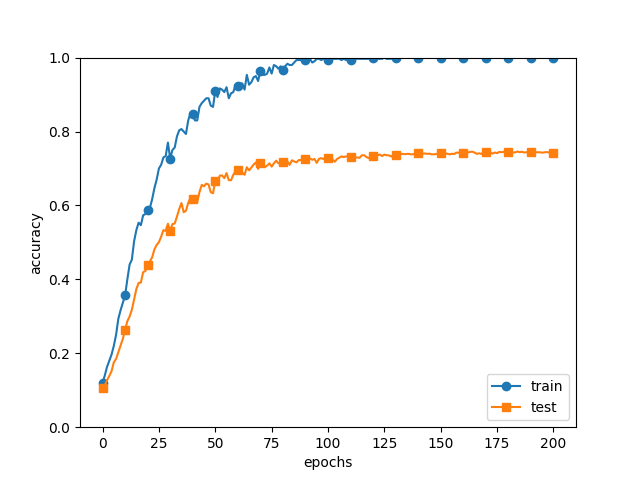 訓練データ(train)とテストデータ(test)の認識精度の推移
訓練データ(train)とテストデータ(test)の認識精度の推移
訓練データを用いて計測した認識精度は、100 エポックを過ぎたあたりから、ほとんど 100% です。しかし、テストデータに対しては100% の認識精度からは大きな隔たりがあります。このような認識精度の大きな隔たりは、訓練データだけに適応しすぎてしまった結果です。
Weight decay:荷重減衰
重みの2重ノルム(L2ノルム)を損失関数に加算してあげれば、重みが大きくなる事を抑えられる(過学習を抑制する)
重みWとすれば、L2ノルムのWeight decayは 1/2 λW2
(λは正則化の強さをコントロールするハイパーパラメータ、大きくするほど大きな重みへのペナルティを課す)
L2ノルム
式
$$ \sqrt{ w _{ 1 } ^{ 2 } + w _{ 2 } ^{ 2 } + ... + w _{ n } ^{ 2 } } $$
L1ノルム
式
$$| w _{ 1 } | + | w _{ 2 } | + \ ... \ + | w _{ n } |$$
荷重限数を使った時、重みの勾配を求める計算では、これまでの誤差逆伝播法による結果に、正則化項の微分 λW を加算
一般的によく用いられる L2 ノルムで実験
(Weight decay に対応したネットワークは common/multi_layer_net.py に、実験用のコードは ch06/overfit_weight_decay.py)
(common/multi_layer_net.py)
import sys, os sys.path.append(os.pardir) # 親ディレクトリのファイルをインポートするための設定 import numpy as np from collections import OrderedDict from common.layers import * from common.gradient import numerical_gradient class MultiLayerNet: """全結合による多層ニューラルネットワーク Parameters ---------- input_size : 入力サイズ(MNISTの場合は784) hidden_size_list : 隠れ層のニューロンの数のリスト(e.g. [100, 100, 100]) output_size : 出力サイズ(MNISTの場合は10) activation : 'relu' or 'sigmoid' weight_init_std : 重みの標準偏差を指定(e.g. 0.01) 'relu'または'he'を指定した場合は「Heの初期値」を設定 'sigmoid'または'xavier'を指定した場合は「Xavierの初期値」を設定 weight_decay_lambda : Weight Decay(L2ノルム)の強さ """ def __init__(self, input_size, hidden_size_list, output_size, activation='relu', weight_init_std='relu', weight_decay_lambda=0.1): # 0から0.1に変える self.input_size = input_size self.output_size = output_size self.hidden_size_list = hidden_size_list self.hidden_layer_num = len(hidden_size_list) self.weight_decay_lambda = weight_decay_lambda self.params = {} # 重みの初期化 self.__init_weight(weight_init_std) # レイヤの生成 activation_layer = {'sigmoid': Sigmoid, 'relu': Relu} self.layers = OrderedDict() for idx in range(1, self.hidden_layer_num+1): self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)], self.params['b' + str(idx)]) self.layers['Activation_function' + str(idx)] = activation_layer[activation]() idx = self.hidden_layer_num + 1 self.layers['Affine' + str(idx)] = Affine(self.params['W' + str(idx)], self.params['b' + str(idx)]) self.last_layer = SoftmaxWithLoss() def __init_weight(self, weight_init_std): """重みの初期値設定 Parameters ---------- weight_init_std : 重みの標準偏差を指定(e.g. 0.01) 'relu'または'he'を指定した場合は「Heの初期値」を設定 'sigmoid'または'xavier'を指定した場合は「Xavierの初期値」を設定 """ all_size_list = [self.input_size] + self.hidden_size_list + [self.output_size] for idx in range(1, len(all_size_list)): scale = weight_init_std if str(weight_init_std).lower() in ('relu', 'he'): scale = np.sqrt(2.0 / all_size_list[idx - 1]) # ReLUを使う場合に推奨される初期値 elif str(weight_init_std).lower() in ('sigmoid', 'xavier'): scale = np.sqrt(1.0 / all_size_list[idx - 1]) # sigmoidを使う場合に推奨される初期値 self.params['W' + str(idx)] = scale * np.random.randn(all_size_list[idx-1], all_size_list[idx]) self.params['b' + str(idx)] = np.zeros(all_size_list[idx]) def predict(self, x): for layer in self.layers.values(): x = layer.forward(x) return x def loss(self, x, t): """損失関数を求める Parameters ---------- x : 入力データ t : 教師ラベル Returns ------- 損失関数の値 """ y = self.predict(x) weight_decay = 0 for idx in range(1, self.hidden_layer_num + 2): W = self.params['W' + str(idx)] weight_decay += 0.5 * self.weight_decay_lambda * np.sum(W ** 2) return self.last_layer.forward(y, t) + weight_decay def accuracy(self, x, t): y = self.predict(x) y = np.argmax(y, axis=1) if t.ndim != 1 : t = np.argmax(t, axis=1) accuracy = np.sum(y == t) / float(x.shape[0]) return accuracy def numerical_gradient(self, x, t): """勾配を求める(数値微分) Parameters ---------- x : 入力データ t : 教師ラベル Returns ------- 各層の勾配を持ったディクショナリ変数 grads['W1']、grads['W2']、...は各層の重み grads['b1']、grads['b2']、...は各層のバイアス """ loss_W = lambda W: self.loss(x, t) grads = {} for idx in range(1, self.hidden_layer_num+2): grads['W' + str(idx)] = numerical_gradient(loss_W, self.params['W' + str(idx)]) grads['b' + str(idx)] = numerical_gradient(loss_W, self.params['b' + str(idx)]) return grads def gradient(self, x, t): """勾配を求める(誤差逆伝搬法) Parameters ---------- x : 入力データ t : 教師ラベル Returns ------- 各層の勾配を持ったディクショナリ変数 grads['W1']、grads['W2']、...は各層の重み grads['b1']、grads['b2']、...は各層のバイアス """ # forward self.loss(x, t) # backward dout = 1 dout = self.last_layer.backward(dout) layers = list(self.layers.values()) layers.reverse() for layer in layers: dout = layer.backward(dout) # 設定 grads = {} for idx in range(1, self.hidden_layer_num+2): grads['W' + str(idx)] = self.layers['Affine' + str(idx)].dW + self.weight_decay_lambda * self.layers['Affine' + str(idx)].W grads['b' + str(idx)] = self.layers['Affine' + str(idx)].db return grads
(ch06/overfit_weight_ decay.py)
weight_decay_lambda を 0-> 1にする
... # weight decay(荷重減衰)の設定 ======================= weight_decay_lambda = 0 # weight decayを使用しない場合 weight_decay_lambda = 0.1 # ==================================================== ...
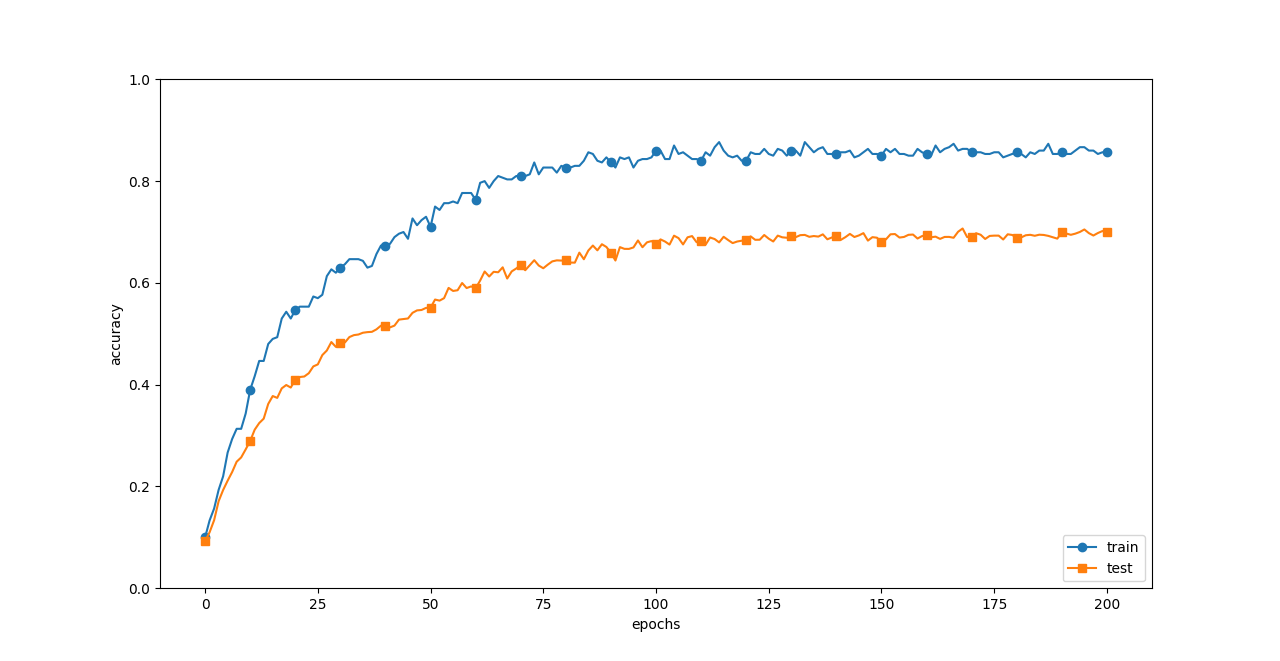 Weight decay を用いた訓練データ(train)とテストデータ(test)の認識精度の推移
Weight decay を用いた訓練データ(train)とテストデータ(test)の認識精度の推移
「訓練データ(train)とテストデータ(test)の認識精度の推移」で描画した時と比較すると、隔たりが小さくなっている。
-> 過学習が抑制されてテストデータの精度が高まった。
訓練データの認識精度が 100%に到達していない
-> 過剰な表現力が和らいだ。
Dropout:ニューロンをランダムに消去しながら学習する手法(過学習を抑制)
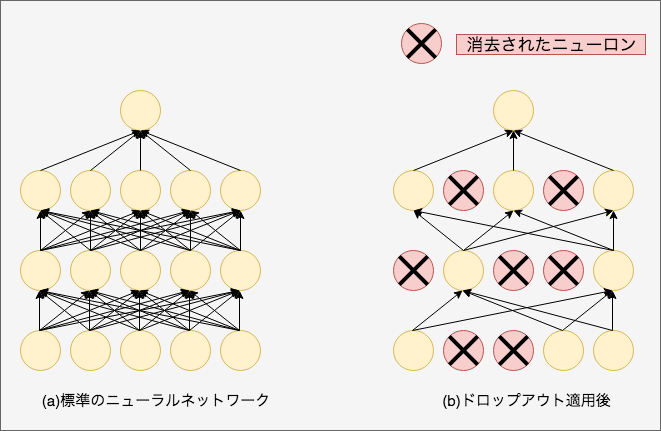 Dropout の概念図(文献 [14] より引用):左が通常のニューラルネットワーク、右が Dropout を適用したネットワーク。Dropout はランダムにニューロンを選び、そのニューロンを消去すること で、その先の信号の伝達をストップする
Dropout の概念図(文献 [14] より引用):左が通常のニューラルネットワーク、右が Dropout を適用したネットワーク。Dropout はランダムにニューロンを選び、そのニューロンを消去すること で、その先の信号の伝達をストップする
class Dropout: def __init__(self, dropout_ratio=0.5): self.dropout_ratio = dropout_ratio self.mask = None def forward(self, x, train_flg=True): if train_flg: self.mask = np.random.rand(*x.shape) > self.dropout_ratio return x * self.mask else: return x * (1.0 - self.dropout_ratio) def backward(self, dout): return dout * self.mask
順伝播
self.mask に消去するニューロンを False として格納するということです。self.mask は、x と同じ形状の配列をランダムに 生成し、その値が dropout_ratio よりも大きい要素だけを True とします。
逆伝播
ReLU と同じです。つまり、順伝播で信号を通したニューロンは、逆伝播の際に伝わる信号をそのまま通し、順伝播で信号を通さなかったニューロンは、逆伝播では信号がそこでストップします。
MNIST データセットで検証(common/trainer.py および ch06/overfit_dropout.py)
trainer.py
import sys, os sys.path.append(os.pardir) # 親ディレクトリのファイルをインポートするための設定 import numpy as np from common.optimizer import * class Trainer: """ニューラルネットの訓練を行うクラス """ def __init__(self, network, x_train, t_train, x_test, t_test, epochs=20, mini_batch_size=100, optimizer='SGD', optimizer_param={'lr':0.01}, evaluate_sample_num_per_epoch=None, verbose=True): self.network = network self.verbose = verbose self.x_train = x_train self.t_train = t_train self.x_test = x_test self.t_test = t_test self.epochs = epochs self.batch_size = mini_batch_size self.evaluate_sample_num_per_epoch = evaluate_sample_num_per_epoch # optimizer optimizer_class_dict = {'sgd':SGD, 'momentum':Momentum, 'nesterov':Nesterov, 'adagrad':AdaGrad, 'rmsprpo':RMSprop, 'adam':Adam} self.optimizer = optimizer_class_dict[optimizer.lower()](**optimizer_param) self.train_size = x_train.shape[0] self.iter_per_epoch = max(self.train_size / mini_batch_size, 1) self.max_iter = int(epochs * self.iter_per_epoch) self.current_iter = 0 self.current_epoch = 0 self.train_loss_list = [] self.train_acc_list = [] self.test_acc_list = [] def train_step(self): batch_mask = np.random.choice(self.train_size, self.batch_size) x_batch = self.x_train[batch_mask] t_batch = self.t_train[batch_mask] grads = self.network.gradient(x_batch, t_batch) self.optimizer.update(self.network.params, grads) loss = self.network.loss(x_batch, t_batch) self.train_loss_list.append(loss) if self.verbose: print("train loss:" + str(loss)) if self.current_iter % self.iter_per_epoch == 0: self.current_epoch += 1 x_train_sample, t_train_sample = self.x_train, self.t_train x_test_sample, t_test_sample = self.x_test, self.t_test if not self.evaluate_sample_num_per_epoch is None: t = self.evaluate_sample_num_per_epoch x_train_sample, t_train_sample = self.x_train[:t], self.t_train[:t] x_test_sample, t_test_sample = self.x_test[:t], self.t_test[:t] train_acc = self.network.accuracy(x_train_sample, t_train_sample) test_acc = self.network.accuracy(x_test_sample, t_test_sample) self.train_acc_list.append(train_acc) self.test_acc_list.append(test_acc) if self.verbose: print("=== epoch:" + str(self.current_epoch) + ", train acc:" + str(train_acc) + ", test acc:" + str(test_acc) + " ===") self.current_iter += 1 def train(self): for i in range(self.max_iter): self.train_step() test_acc = self.network.accuracy(self.x_test, self.t_test) if self.verbose: print("=============== Final Test Accuracy ===============") print("test acc:" + str(test_acc))
overfit_dropout.py
ドロップアウト無し
import os import sys sys.path.append(os.pardir) # 親ディレクトリのファイルをインポートするための設定 import numpy as np import matplotlib.pyplot as plt from dataset.mnist import load_mnist from common.multi_layer_net_extend import MultiLayerNetExtend from common.trainer import Trainer (x_train, t_train), (x_test, t_test) = load_mnist(normalize=True) # 過学習を再現するために、学習データを削減 x_train = x_train[:300] t_train = t_train[:300] # Dropuoutの有無、割り合いの設定 ======================== use_dropout = False # Dropoutなしのときの場合はFalseに dropout_ratio = 0.2 # ==================================================== network = MultiLayerNetExtend(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100], output_size=10, use_dropout=use_dropout, dropout_ration=dropout_ratio) trainer = Trainer(network, x_train, t_train, x_test, t_test, epochs=301, mini_batch_size=100, optimizer='sgd', optimizer_param={'lr': 0.01}, verbose=True) trainer.train() train_acc_list, test_acc_list = trainer.train_acc_list, trainer.test_acc_list # グラフの描画========== markers = {'train': 'o', 'test': 's'} x = np.arange(len(train_acc_list)) plt.plot(x, train_acc_list, marker='o', label='train', markevery=10) plt.plot(x, test_acc_list, marker='s', label='test', markevery=10) plt.xlabel("epochs") plt.ylabel("accuracy") plt.ylim(0, 1.0) plt.legend(loc='lower right') plt.show()
ドロップアウト有り
# Dropuoutの有無、割り合いの設定 ========================
use_dropout = True# False->Trueに変える
dropout_ratio = 0.2
# ====================================================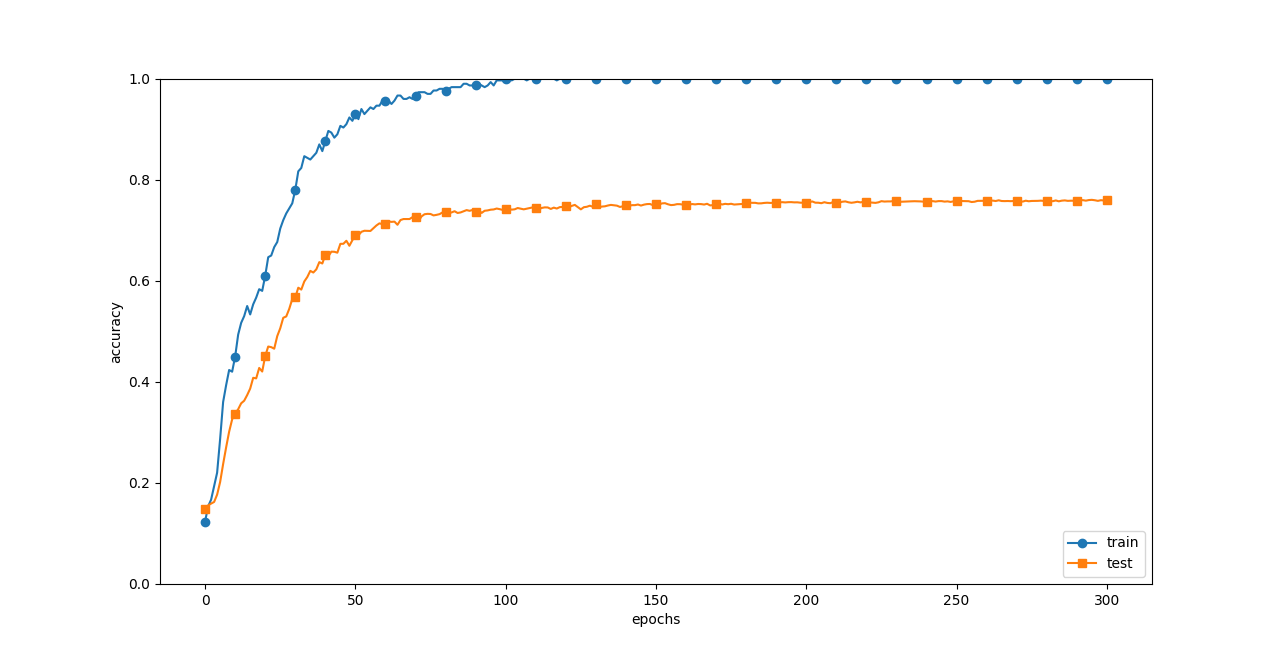 ドロップアウト無し
ドロップアウト無し
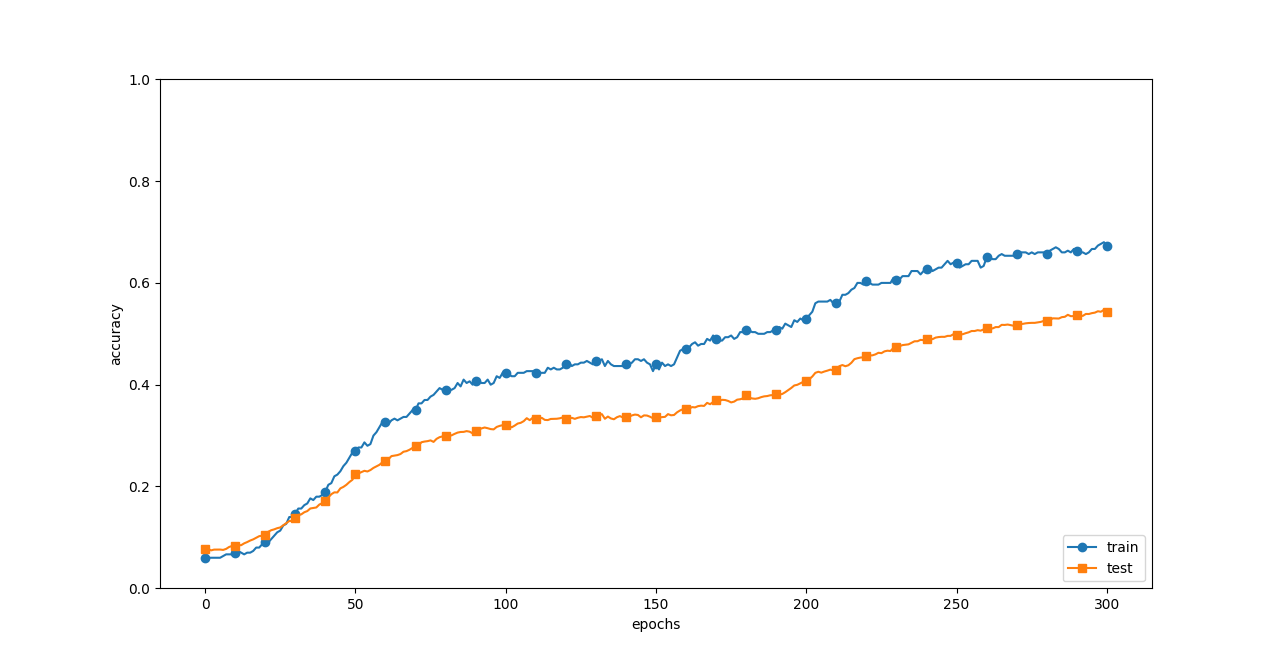 ドロップアウト有り(dropout_ratio = 0.2)
ドロップアウト有り(dropout_ratio = 0.2)
ドロップアウト有りの時の方が訓練データとテストデータの隔たりが小さくなった。
これまでのハイパーパラメータ例
・各層のニューロンの数
・バッチサイズ
・学習係数
・Weight decay
ハイパーパラメータはテストデータで性能を評価してはいけない
→過学習を起こす起こす事になるから(テストデータだけに適合するようにハイパーパラメータの値が調整されてしまう)
データセットによっては、あらかじめ訓練データ・検証データ・テストデータの 3つに分離されているものもあるが、訓練データとテストデータだけのものもある。
訓練データの中から 20% 程度を検証データとして先に分離する
(x_train, t_train), (x_test, t_test) = load_mnist() # 訓練データをシャッフル x_train, t_train = shuffle_dataset(x_train, t_train) # 検証データの分割 validation_rate = 0.20 validation_num = int(x_train.shape[0] * validation_rate) x_val - x_train[:validation_num] t_val - t_train[:validation_num] x_train - x_train[validation_num:] t_train - t_train[validation_num:]
ハイパーパラメータの最適化には次のステップを繰り返す
STEP0
ハイパーパラメータの範囲を指定する:最初はざっくりと指定(例: 10-3から103)
STEP1
設定されたハイパーパラメータの範囲からランダムにサンプリングする
STEP2
STEP1でサンプリングされたハイパーパラメータの値を使用して学習を行い、
喧騒データの認識精度を評価する
(ただし、エポックは小さく設定)
STEP3
STEP2とSTEP2 をある回数(100回など)繰り返し、それらの認識精度の結果から
ハイパーパラメータの範囲を狭める
上記を繰り返し行い、ハイパーパラメータの範囲を絞り込んでいき、ある程度絞り込んだ段階で、その絞り込んだ範囲からハイパーパラメータの値をひとつ選び出す。
ハイパーパラメータのランダムサンプリング(Weight decay係数 10-8~10-4, 学習係数 10-6~10-2)
wight_decay = 10 ** np.random.uniform(-8, -4) lr = 10 ** np.random.uniform(-6, -2)
(ch06/hyperparameter_optimization.py)
import sys, os
sys.path.append(os.pardir) # 親ディレクトリのファイルをインポートするための設定
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.multi_layer_net import MultiLayerNet
from common.util import shuffle_dataset
from common.trainer import Trainer
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)
# 高速化のため訓練データの削減
x_train = x_train[:500]
t_train = t_train[:500]
# 検証データの分離
validation_rate = 0.20
validation_num = int(x_train.shape[0] * validation_rate)
x_train, t_train = shuffle_dataset(x_train, t_train)
x_val = x_train[:validation_num]
t_val = t_train[:validation_num]
x_train = x_train[validation_num:]
t_train = t_train[validation_num:]
def __train(lr, weight_decay, epocs=50):
network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100],
output_size=10, weight_decay_lambda=weight_decay)
trainer = Trainer(network, x_train, t_train, x_val, t_val,
epochs=epocs, mini_batch_size=100,
optimizer='sgd', optimizer_param={'lr': lr}, verbose=False)
trainer.train()
return trainer.test_acc_list, trainer.train_acc_list
# ハイパーパラメータのランダム探索======================================
optimization_trial = 100
results_val = {}
results_train = {}
for _ in range(optimization_trial):
# 探索したハイパーパラメータの範囲を指定===============
weight_decay = 10 ** np.random.uniform(-8, -4)
lr = 10 ** np.random.uniform(-6, -2)
# ================================================
val_acc_list, train_acc_list = __train(lr, weight_decay)
print("val acc:" + str(val_acc_list[-1]) + " | lr:" + str(lr) + ", weight decay:" + str(weight_decay))
key = "lr:" + str(lr) + ", weight decay:" + str(weight_decay)
results_val[key] = val_acc_list
results_train[key] = train_acc_list
# グラフの描画========================================================
print("=========== Hyper-Parameter Optimization Result ===========")
graph_draw_num = 20
col_num = 5
row_num = int(np.ceil(graph_draw_num / col_num))
i = 0
for key, val_acc_list in sorted(results_val.items(), key=lambda x:x[1][-1], reverse=True):
print("Best-" + str(i+1) + "(val acc:" + str(val_acc_list[-1]) + ") | " + key)
plt.subplot(row_num, col_num, i+1)
plt.title("Best-" + str(i+1))
plt.ylim(0.0, 1.0)
if i % 5: plt.yticks([])
else: plt.yticks(np.arange(0.0, 1.2, 0.2))
plt.xticks([])
x = np.arange(len(val_acc_list))
plt.plot(x, val_acc_list)
plt.plot(x, results_train[key], "--")
i += 1
if i >= graph_draw_num:
break
plt.show()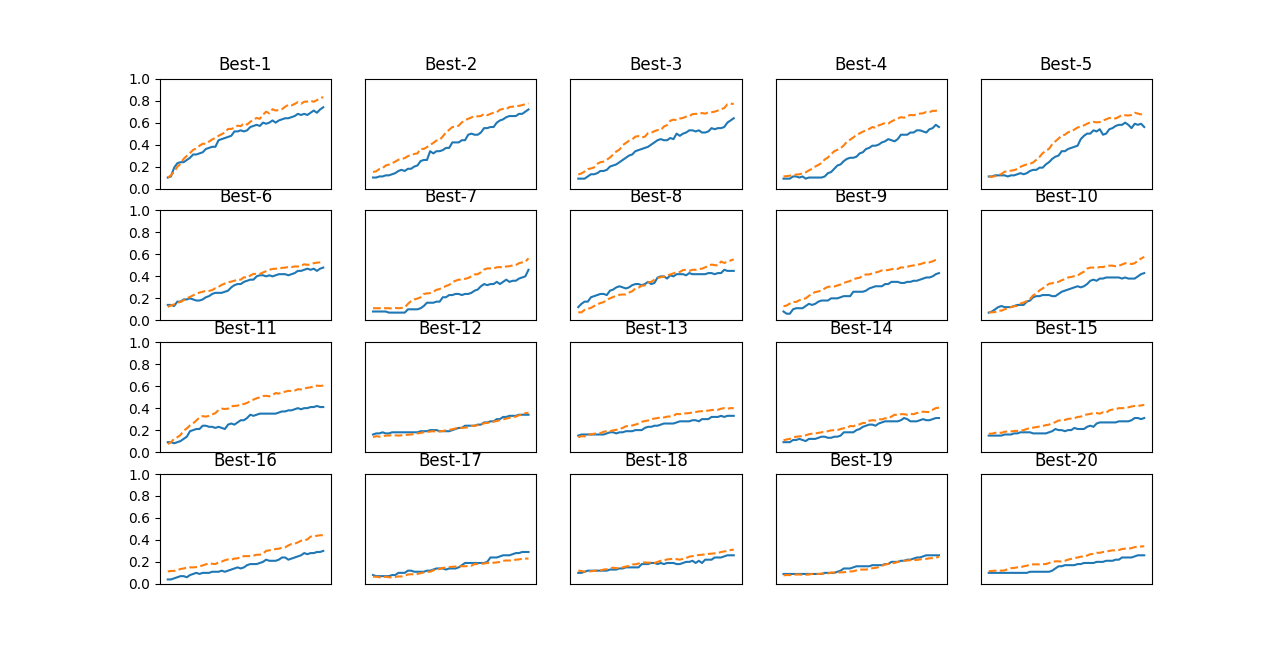 実線は検証データの認識精度、点線は訓練データの認識精度
実線は検証データの認識精度、点線は訓練データの認識精度
これを見ると、「Best-5」ぐらいまでは順調に学習が進んでいることが分かります。
そこで、「Best-5」までのハイパーパラメータの値(学習係数と Weight decay 係数) を見てみることにします。
結果は、次のようになります。
=========== Hyper-Parameter Optimization Result ===========
Best-1(val acc:0.74) | lr:0.006122975949705087, weight decay:4.690616950485899e-06
Best-2(val acc:0.72) | lr:0.005573546740364351, weight decay:2.9035359797864116e-06
Best-3(val acc:0.64) | lr:0.006482289721036491, weight decay:7.200405044009874e-06
Best-4(val acc:0.56) | lr:0.003986587050968818, weight decay:2.0943590408712787e-06
Best-5(val acc:0.56) | lr:0.004401355290764625, weight decay:1.6830975160518582e-08
この結果を見ると、うまく学習が進んでいるのは、学習係数が 0.001 から 0.01、 Weight decay 係数が 10-8から 10-6 ぐらいということが分かります。よって、学習係数の幅とWeight decayの幅を変更し、再度絞り込みを繰り返します。
weight_decay = 10 ** np.random.uniform(-8, -6)
lr = 10 ** np.random.uniform(-4, -2)
このように、 うまくいきそうなハイパーパラメータの範囲を観察し、値の範囲を小さくしていく作業を繰り返していくのです。
そのようにし て、適切なハイパーパラメータの存在範囲を狭め、ある段階で最終的なハイパラメータの値をひとつピックアップします。
● パラメータの更新方法には、SGD の他に、有名なものとして、Momentum や AdaGrad、Adam などの手法がある。
● 重みの初期値の与え方は、正しい学習を行う上で非常に重要である。
● 重みの初期値として、「Xavier の初期値」や「He の初期値」などが有効
である。
● Batch Normalization を用いることで、学習を速く進めることができ、ま
た、初期値に対してロバストになる。
● 過学習を抑制するための正則化の技術として、Weight decay や Dropout
がある。
● ハイパーパラメータの探索は、良い値が存在する範囲を徐々に絞りながら
進めるのが効率の良い方法である。