Ruby マージソート

マージソートとは

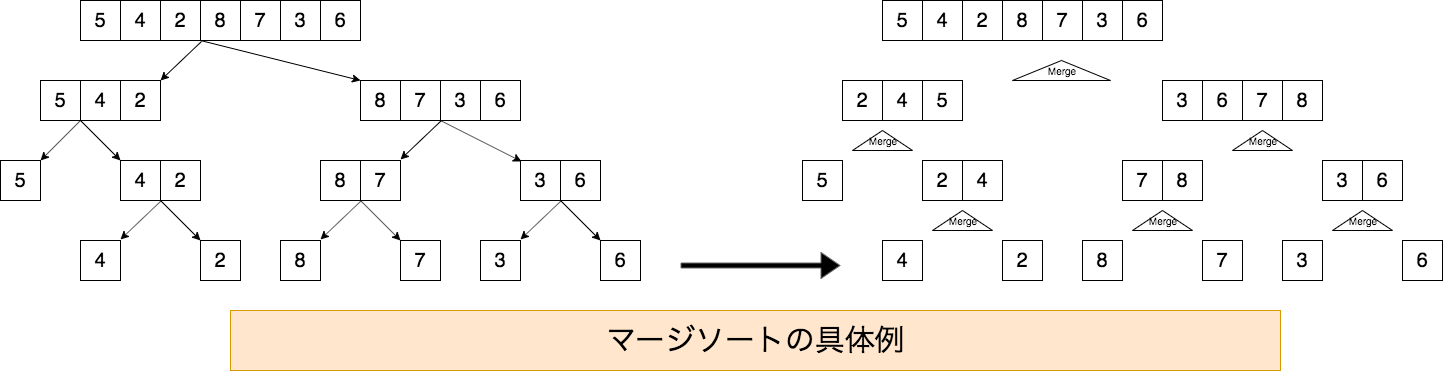
マージソートは、ソートのアルゴリズムで、既に整列してある複数個の列を1個の列にマージする際に、小さいものから先に新しい列に並べれば、新しい列も整列されている、というボトムアップの分割統治法による。大きい列を多数の列に分割し、そのそれぞれをマージする作業は並列化できる。

n個のデータを含む配列をソートする場合、最悪計算量O(n log n)である。分割と統合の実装にもよるが、一般に安定なソートを実装できる。インプレースな（すなわち入力の記憶領域を出力にも使うので、追加の作業記憶領域を必要としない）バリエーションも提案されているが、一般には、O(n)の追加の作業記憶領域を必要とする。

（ナイーブな）クイックソートと比べると、最悪計算量は少ない。ランダムなデータでは通常、クイックソートのほうが速い。

[wikipedea引用]

アルゴリズム

1. 先頭から順に見ていって、左右の並びがおかしいところがあれば、入れ替える。

2. 最後までたどり着いたら再び先頭に戻って、同じように見ていく。

3. 1度も並び替えをすることなく先頭から最後まで見終わったら完了。

実装

class MergeSort
  def initialize( n )
    @target = Array.new(n)
  end
  
  def main
    puts "準備中"
    
    @target.each_index do |i|
      @target[i] = rand(1000)
    end
    
    p @target
    
    puts "並び替え開始"
    mergeSort(@target.size, @target, 0)
    puts "終了"
    
    p @target
  end
  
  private
  # ----- ソートアルゴリズム
  def mergeSort( n, x, offset )
    return if n <= 1
    m = n / 2
    # ブロックを2分割する
    mergeSort(m, x, offset)
    mergeSort(n - m, x, offset + m)
    
    # 併合操作
    # 分割した左側をbufferにメモ
    buffer = Array.new(m)
    buffer = x[offset, m]
    
    # iは左半分のインデックス
    # jは右半分のインデックス
    # kはxのインデックス
    i, j, k = 0, m, 0
    
    # 左半分と右半分のデータ列の先頭同士を比べ、小さい方をデータ列から取り出して更新
    while (i < m && j < n) do
      if buffer[i] <= x[offset + j]
        x[offset + k] = buffer[i]
        i += 1
      else
        x[offset + k] = x[offset + j]
        j += 1
      end
      k += 1
    end
    
#    if i == m # 左半分をxに移動し尽くした場合、右半分も順番にxに入れていく
#        while (j < n) do
#            x[offset + k] = x[offset + j]
#            k += 1
#            j += 1
#        end
#    else
#        while (i < m) do # 右半分をxに移動し尽くした場合、左半分も順番にxに入れていく
#            x[offset + k] = buffer[i]
#            k += 1
#            i += 1
#        end
#    end

    # 上記の代わりにこっちを使う
    while (i < m) do # 右半分をxに移動し尽くしたので、左半分も順番にxに入れていく
      x[offset + k] = buffer[i]
      k += 1
      i += 1
    end
    
    p x
  end
end


N = 10
merge = MergeSort.new(N)
merge.main

<実行結果>

並び替え開始
[188, 543, 805, 241, 421, 996, 417, 95, 912, 771]
[188, 543, 805, 241, 421, 996, 417, 95, 912, 771]
[188, 543, 241, 421, 805, 996, 417, 95, 912, 771]
[188, 241, 421, 543, 805, 996, 417, 95, 912, 771]
[188, 241, 421, 543, 805, 417, 996, 95, 912, 771]
[188, 241, 421, 543, 805, 417, 996, 95, 771, 912]
[188, 241, 421, 543, 805, 417, 996, 95, 771, 912]
[188, 241, 421, 543, 805, 95, 417, 771, 912, 996]
[95, 188, 241, 417, 421, 543, 771, 805, 912, 996]
終了
[95, 188, 241, 417, 421, 543, 771, 805, 912, 996]

上記のコメントした部分

#    if i == m # 左半分をxに移動し尽くした場合、右半分も順番にxに入れていく
# while (j < n) do
# x[offset + k] = x[offset + j]
# k += 1
# j += 1
# end
# else
# while (i < m) do # 右半分をxに移動し尽くした場合、左半分も順番にxに入れていく
# x[offset + k] = buffer[i]
# k += 1
# i += 1
# end
# end

これは、分割した左半分と右半分のデータ列の先頭同士を比べ、小さい方をデータ列から取り出して更新するときに、先に左側がなくなった場合、残りの右側を余ったインデックスに入れ、逆に先に右がなくなった場合、残りの左側を余ったインデックスに入れるという処理である。

しかしこれは以下コードで代用した。

while (i < m) do # 右半分をxに移動し尽くしたので、左半分も順番にxに入れていく
x[offset + k] = buffer[i]
k += 1
i += 1
end

この処理は、先ほどの処理から、左側を移動し尽くした場合の処理が抜けただけの処理である。

マージソートで大事なのは、1度でもマージされたブロックの要素は昇順になっていることである。

左側を移動し尽くした場合、右側が余るが、すでに余った要素は配列の最後のインデックスまで大きい順で並んであるため、更新する必要はなく、結果は変わらない。

であれば、無駄な処理を省いた後者のコードを採用した。