

updated on 2020-06-20

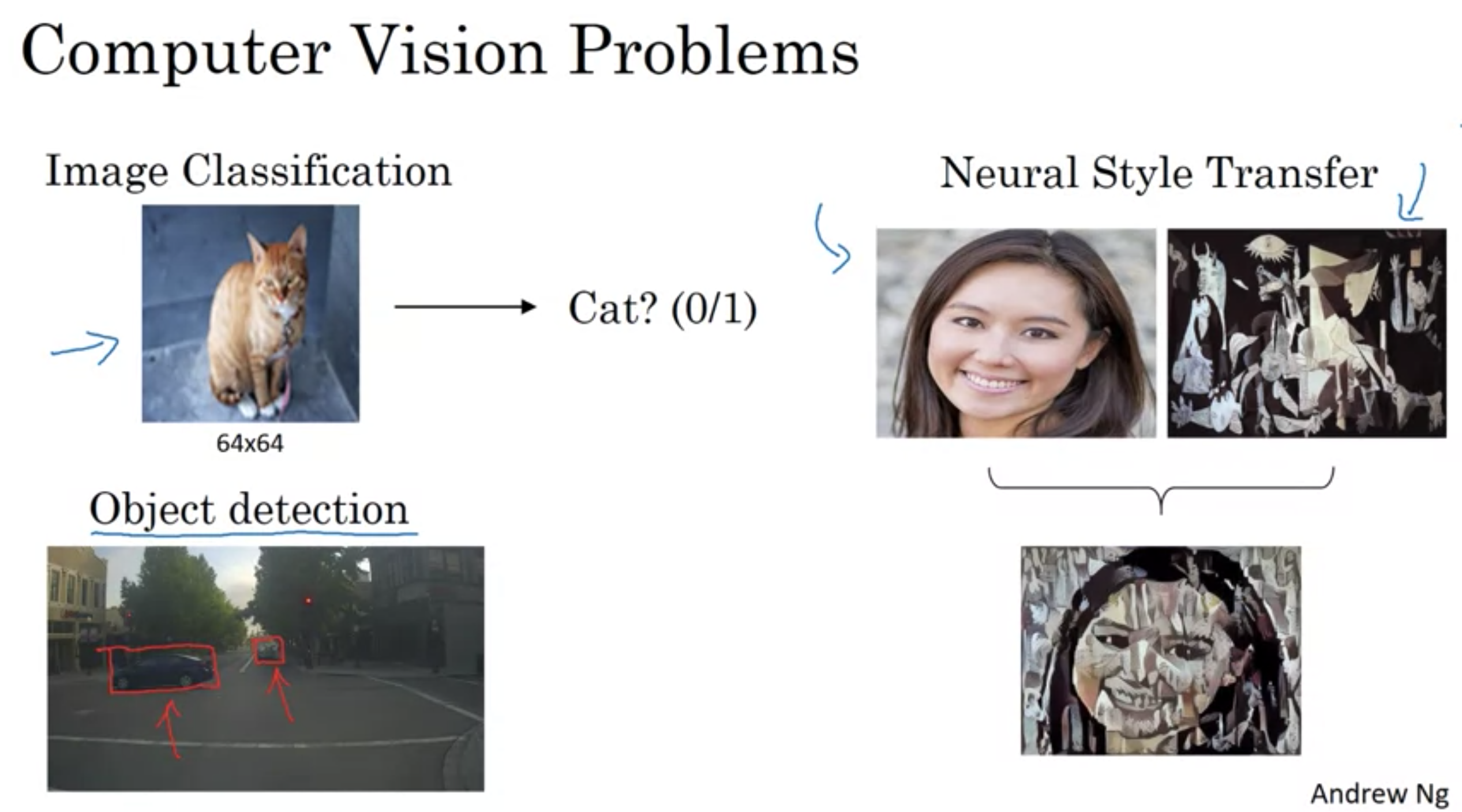
コンピュータビジョン(computer vision)はコンピュータがデジタルな画像、または動画をいかによく理解できるか、ということを扱う研究分野である。 工学的には、人間の視覚システムが行うことができるタスクを自動化することを追求する分野である。(wikipedia引用)
・コンピュータビジョンの急速な進歩により、数年前には無理だった、まったく新しいアプリケーションを表示できるようになった。
・コンピュータビジョンシステム自体を構築しなくても、コンピュータビジョンの研究コミュニティは新しいニューラルネットワークアーキテクチャとアルゴリズムを考案ことに創造的で独創的なため、他の領域への相互交流を作る刺激がある。
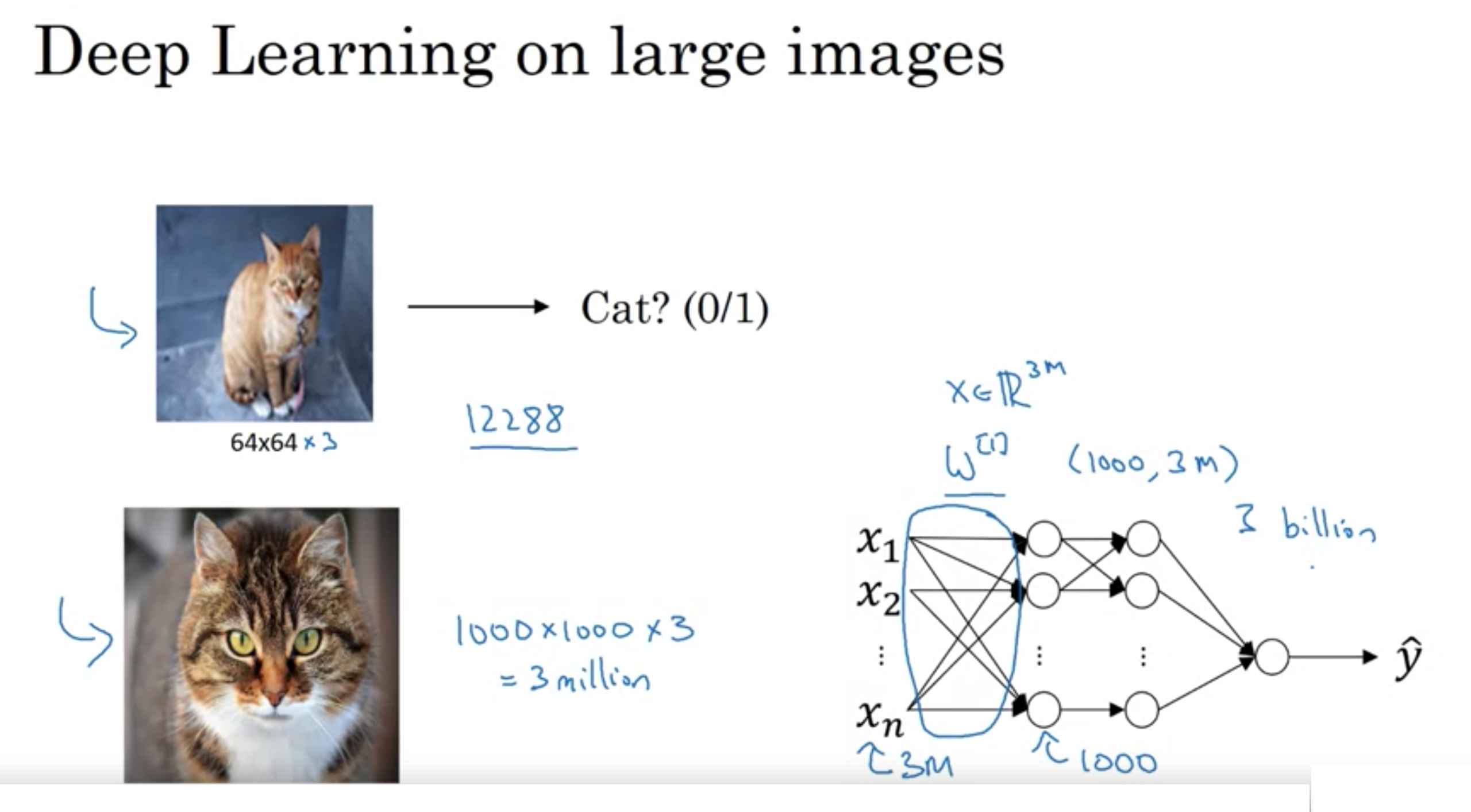
画像が大きい場合、例えば、(幅、高さ、チャンネル数) => (1000px, 1000px, 3)の時、入力\(x \in R ^{ n }\)
仮に一層目のユニットが1000の時、一層目の重みのパラメータは3億個になり、ニューラルネットワークを過学習から防ぐのに十分なデータを得るのが難しい。
また、メモリや計算リソースを満たすのは無理である。
そこで、畳み込み処理を実装する。
[実数空間]
任意の自然数 n に対し、実数の n組の全体からなる集合 \(R ^{ n }\) を「n-次元実数空間」("n-dimensional real space") と呼ぶ。\(R ^{ n }\) の元は、各 \(x _{ i }\) を実数として\(x =(x_{1},x_{2},\ldots ,x_{n})\)と書かれる
各 n に対して数空間\(R ^{ n }\) はただ一つ存在する (wikipedia引用)
画像の中にあるエッジをどの用意検出するか
物体検出が最初に行うことは、画像の垂直または水平のエッジを検出
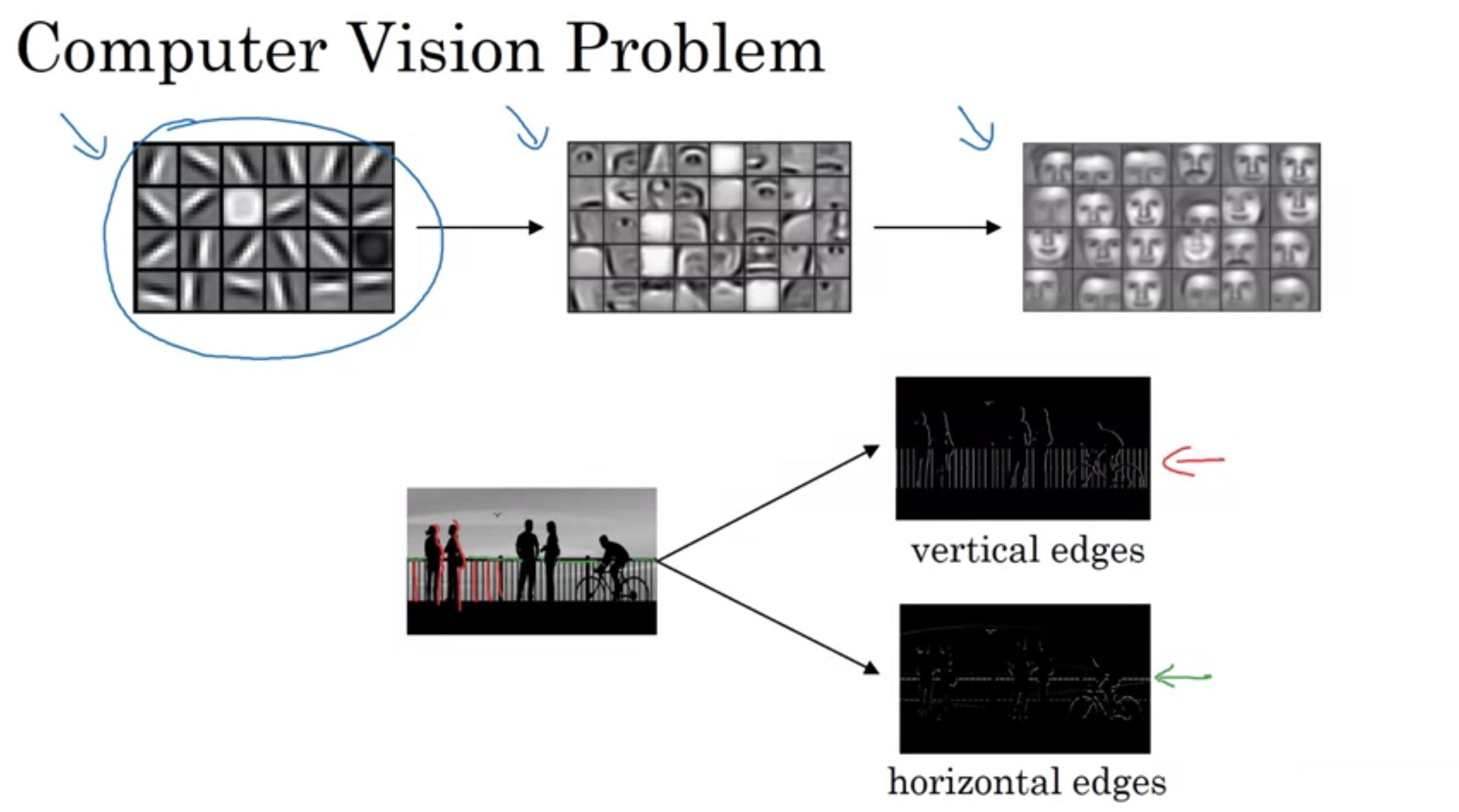
垂直のエッジを検出
(幅,高さ,チャンネル)=(6px,6px,1)のグレースケールの画像を(幅,高さ)=(3,3)のフィルター(研究論文ではカーネルと呼ぶ)で畳み込む
畳み込みは*を用いるが、pythonではかけ算を意味するので、意味の違いに注意
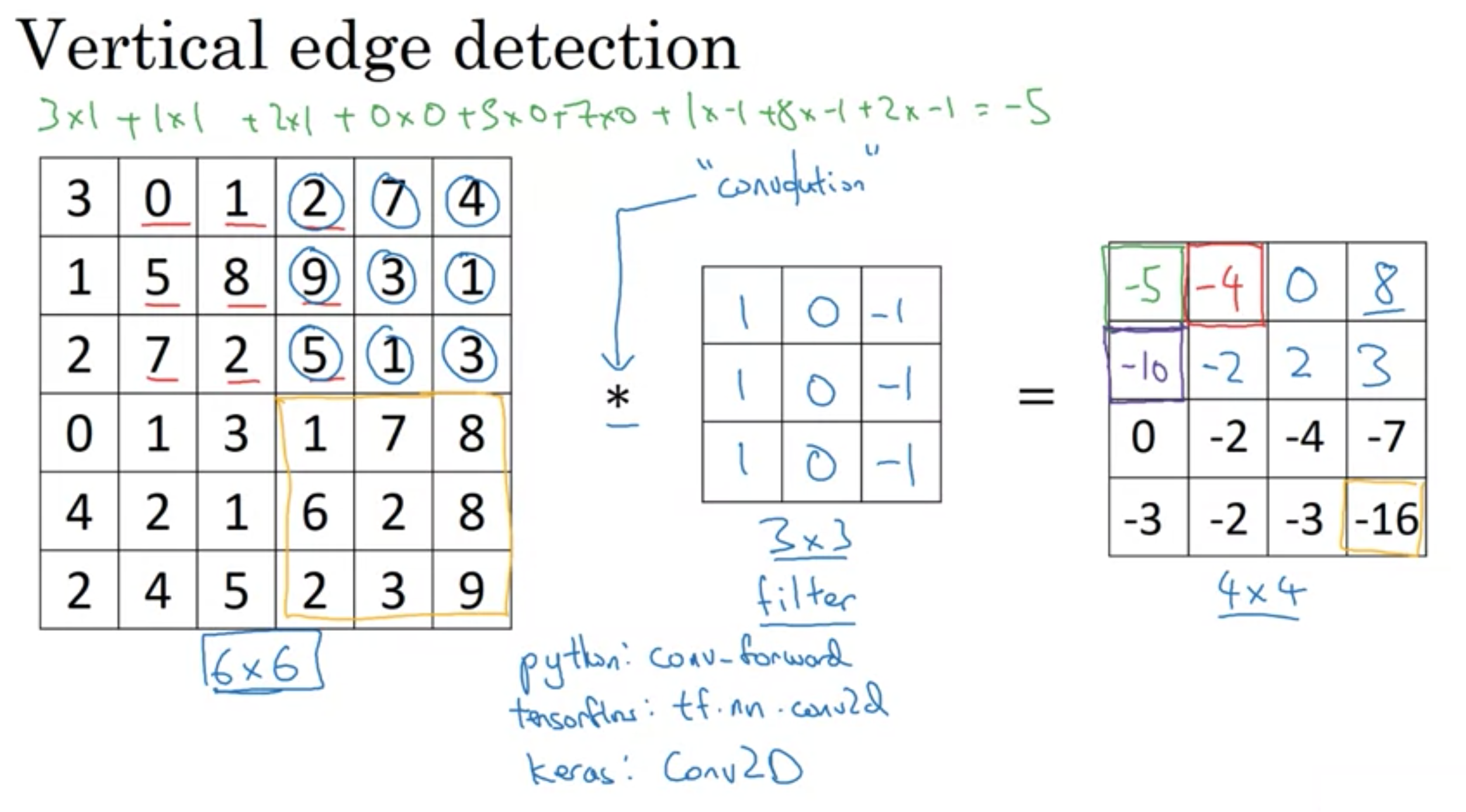 画像の畳み込み
画像の畳み込み
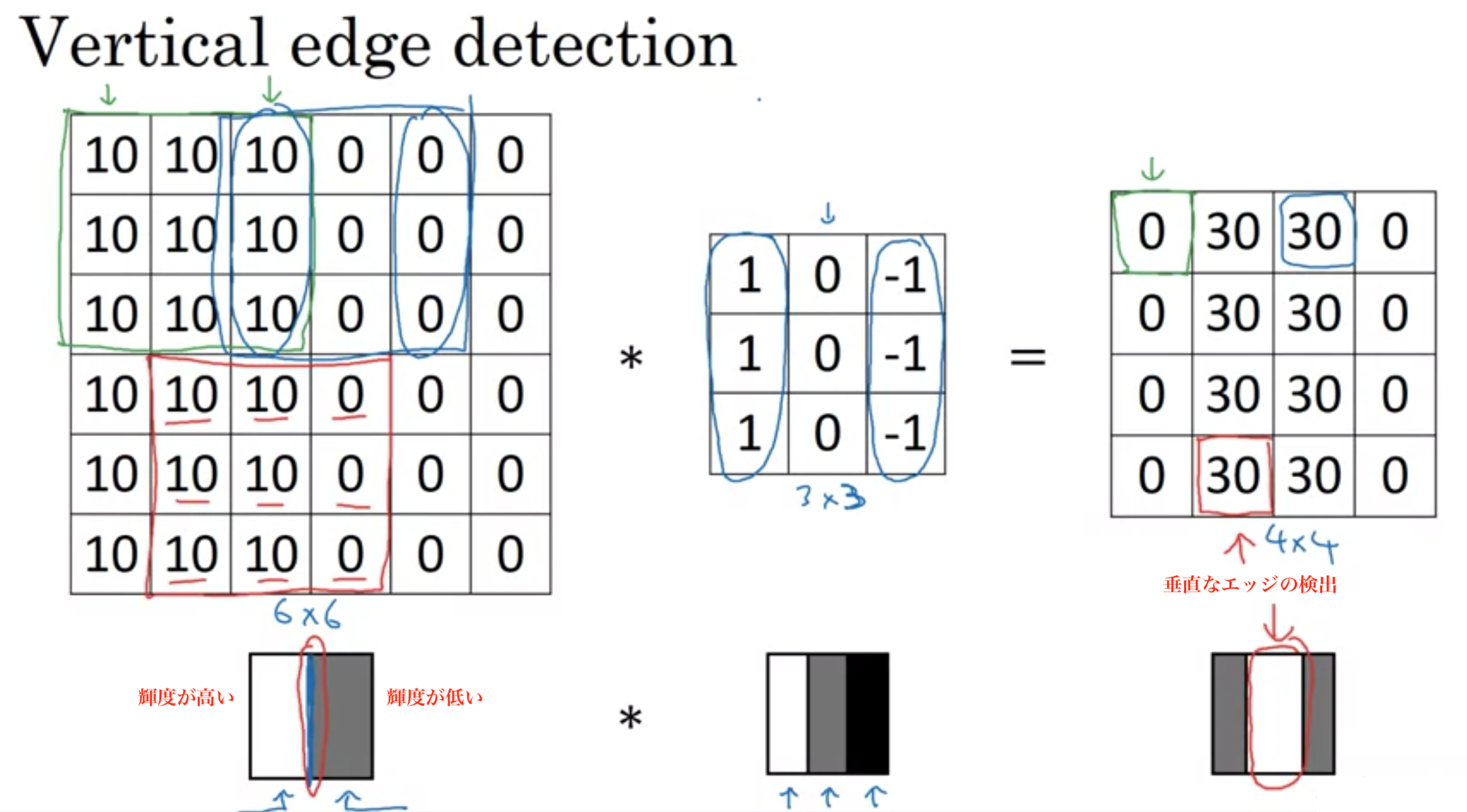 畳み込みによる垂直エッジ検出
畳み込みによる垂直エッジ検出
上記画像では垂直エッジが太く感じるが、フィルターをする画像のサイズを大きくすれば、エッジの太さは変わらないので細く見える。
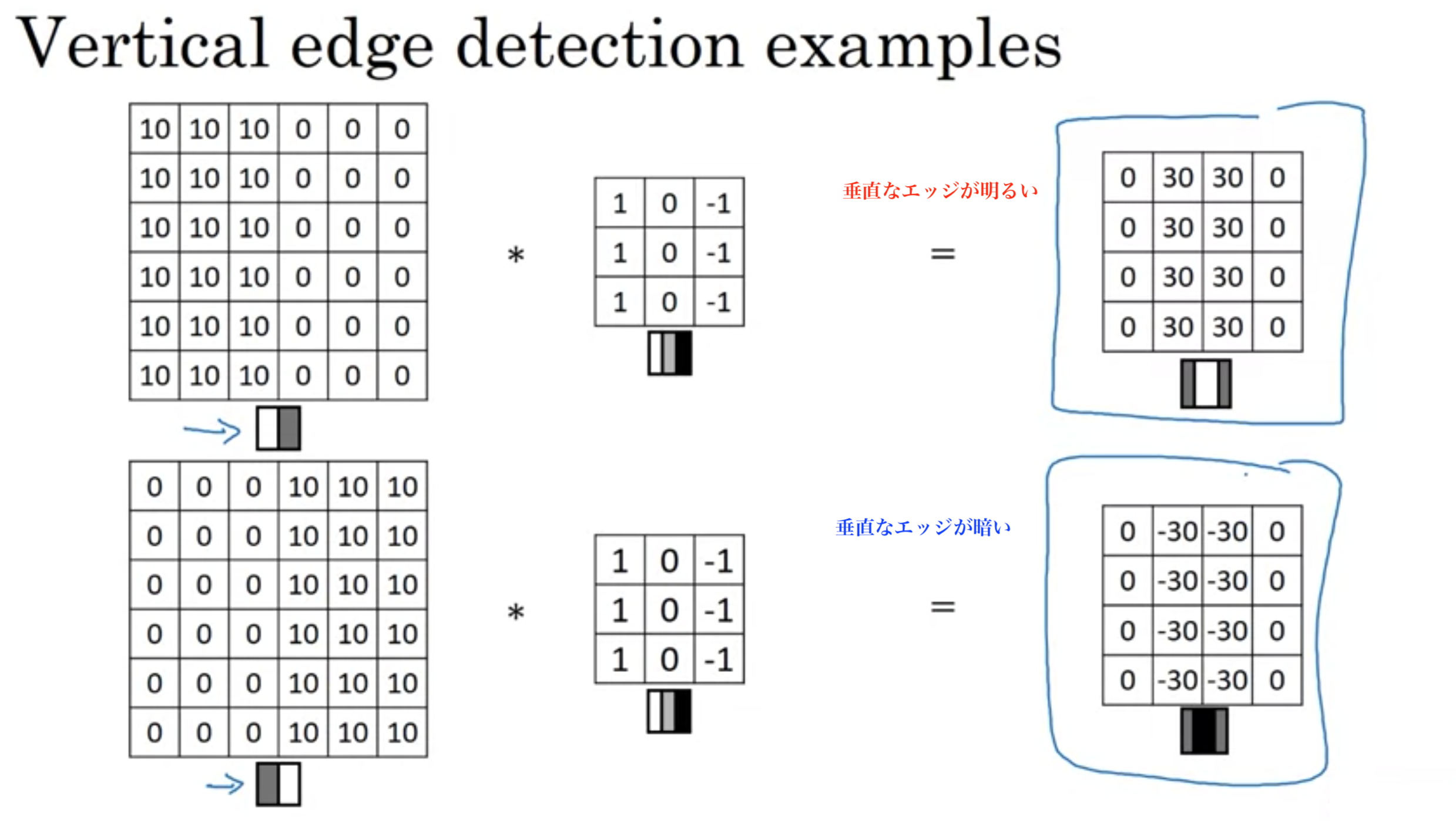 垂直エッジ検出の例
垂直エッジ検出の例
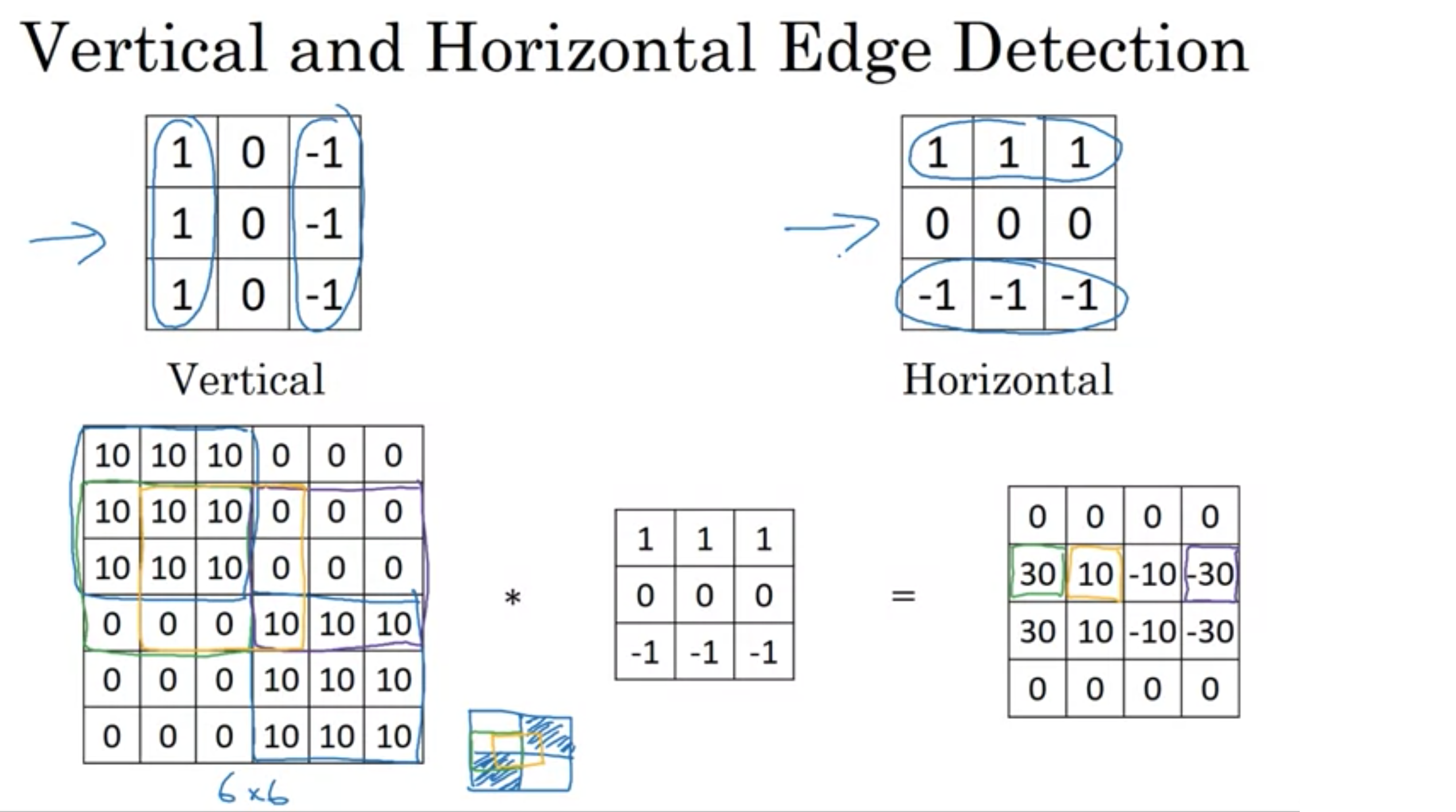 垂直エッジと水平エッジの検出
垂直エッジと水平エッジの検出
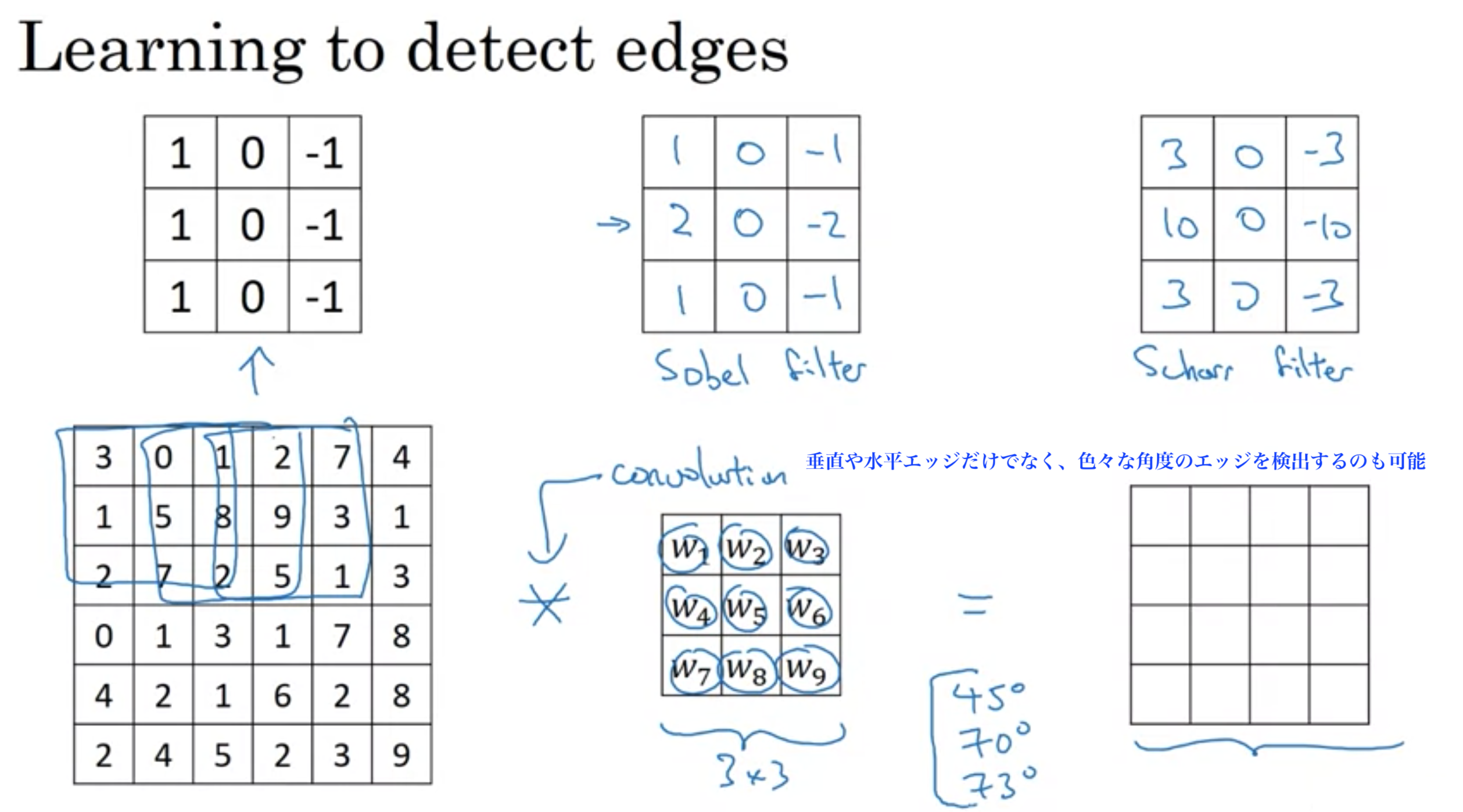
エッジ検出フィルターの数字の組み合わせは色々なものがある。
ソーベルフィルター (Sobel filter)、シャーフィルター (Scharr filter)
垂直エッジフィルターを90度回転させれば水平エッジフィルターになる
幅×高さが6×6の画像を3×3のフィルターで畳み込むと4×4の画像になった。
しかし、畳み込みには2つの欠点がある。
1に関して、100層のニューラルネットワークの場合、各層の出力で画像が縮み、100層後には非常に小さな画像になってしまう。
2に関して、画像の端にある多くの情報を捨ててしまうこと。
この2つを解決する方法がパディング
画像に追加の枠を充てることで、出力画像のサイズを調整することができる。パディング は通常0で埋める。
幅×高さが6×6の画像を3×3のフィルターで畳み込むと4×4の画像に縮むが、畳み込む前に入力画像にパディング 1を適用することで、8×8の画像にフィルターを適用することになり、出力は6×6になり、入力と同じサイズを保持できる。また、角の情報も内部同様オーバーラップした計算を適用できる。
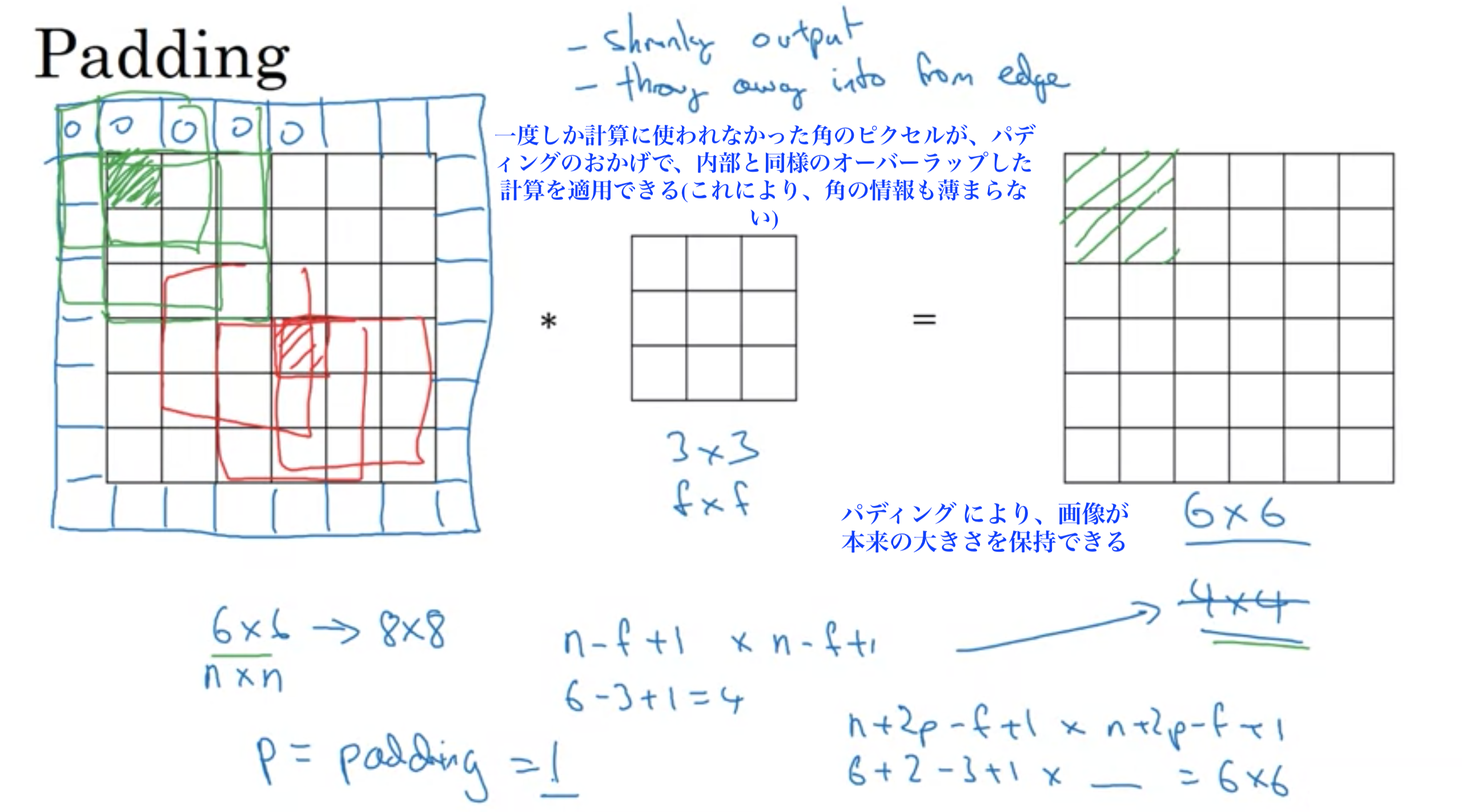
Valid Convolution and Same Convolution
Valid Convolution:
パディングなし 入力(n×n) * フィルター(f×f) => 出力((n-f+1)×(n-f+1))
例: 6×6 * 3×3 => 4×4
Same Convolution:
出力のサイズが入力と同じになるようにパディング
パディング後 ((n+2p)×(n+2p)) * フィルター(f×f) => 出力((n+2p-f+1)×(n+2p-f+1))
出力が入力と同じサイズになるようにパディングするので、n+2p-f+1=nを満たすようにパディングpを決める
つまり、p=\( \dfrac{ f-1 }{ 2 } \) (fは基本奇数)
例: (6+2・1)×(6+2・1) * 3×3 => 6×6
 Valid Convolution and Same Convolution
Valid Convolution and Same Convolution
フィルタをずらしていく幅
7×7の画像を3×3フィルターで畳み込む ストライド=2の時、出力3×3
パディング pの時、入力(n×n) * フィルター(f×f) => 出力(( \( \dfrac{ n+2p-f }{ s } +1 \) )×( \( \dfrac{ n+2p-f }{ s } +1 \) ))
出力のサイズが分数となるときは、小数部分を切り捨てて、もっとも近い整数にする(floor)
ストライドは、画像からはみ出さない範囲でずらしていき、角まで綺麗にずらさない場合は計算しない。
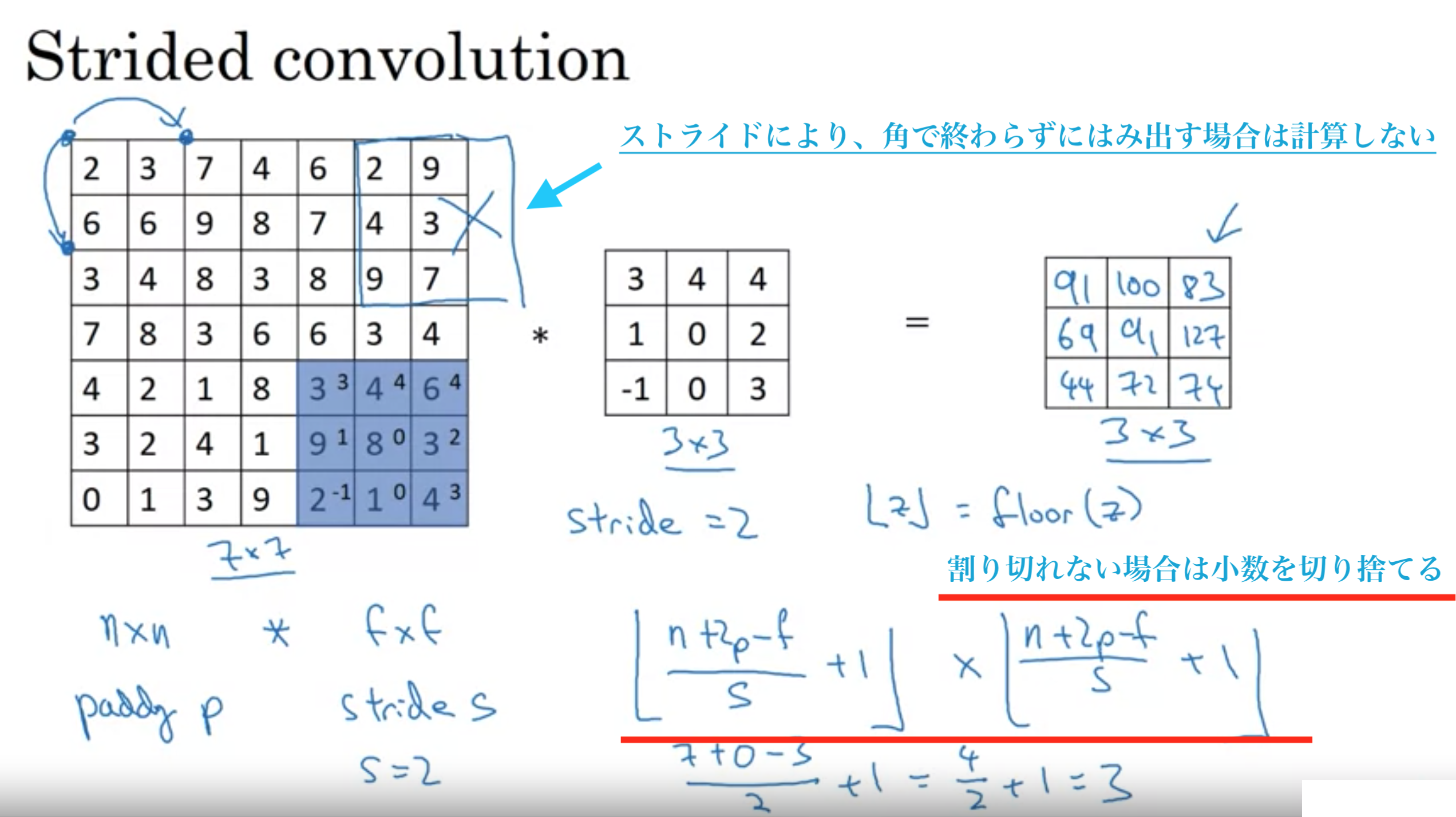 ストライドされた畳み込み
ストライドされた畳み込み
 畳み込みのまとめ
畳み込みのまとめ
技術的注意事項
畳み込みニューラルネットワークを実装するための技術に相互相関がある。
フィルターを水平軸と鉛直軸でひっくり返す。
技術的には、相互相関 (cross-correlation)というが、ディープラーニングの文献では単に畳み込み処理と呼ぶ。
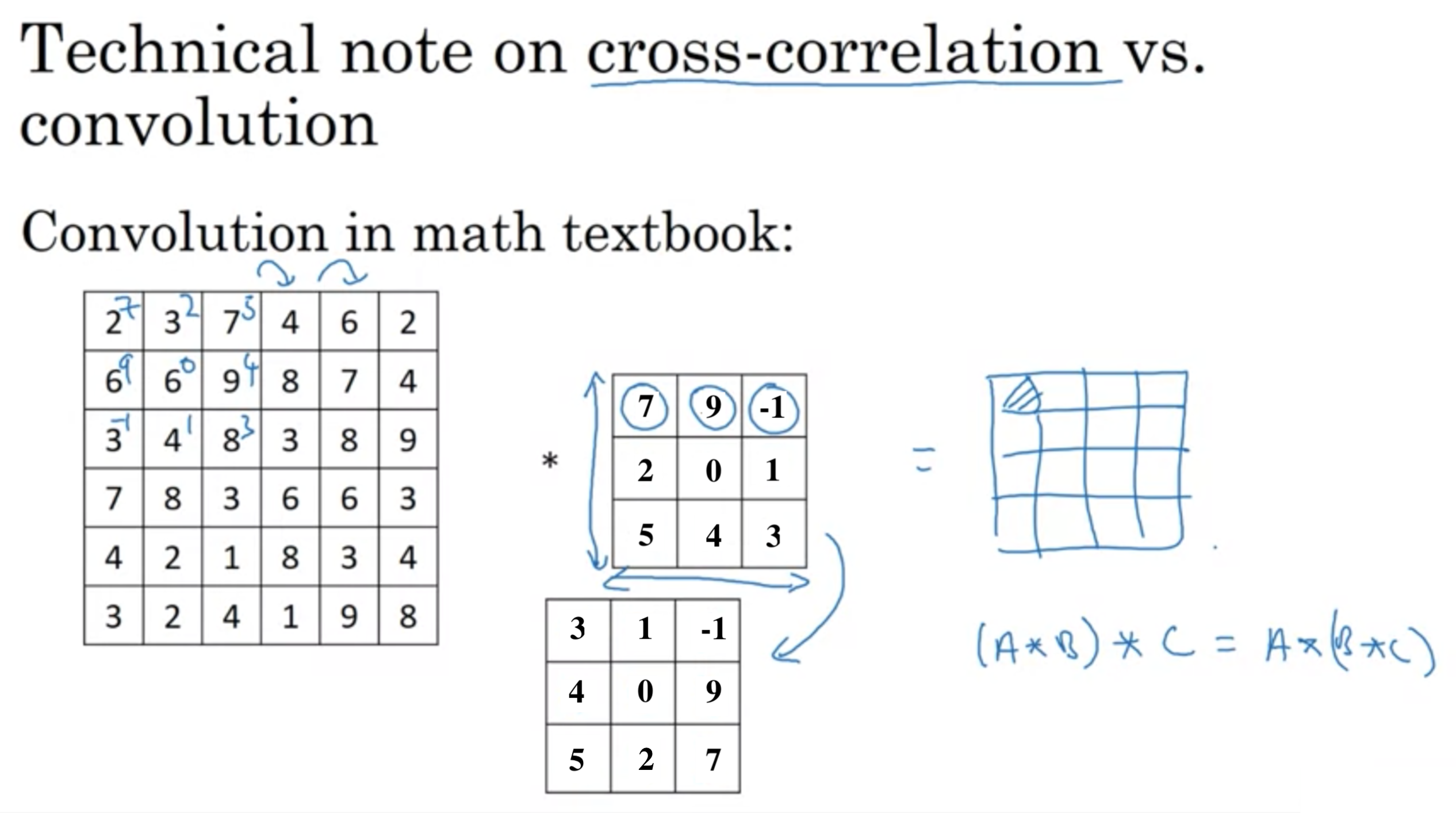 相互相関と畳み込みに関する技術メモ
相互相関と畳み込みに関する技術メモ
グレースケールではなく、有色(RGBが設定された)画像の場合、入力画像の3次元目(チャンネル数)とフィルターの3次元目は同じ数でんければならない
例: 高さ×幅×チャンネル数=6×6×3 の画像
\( 6×6× \dot{ 3 } \ast 3×3× \dot{ 3 }=4×4 \)
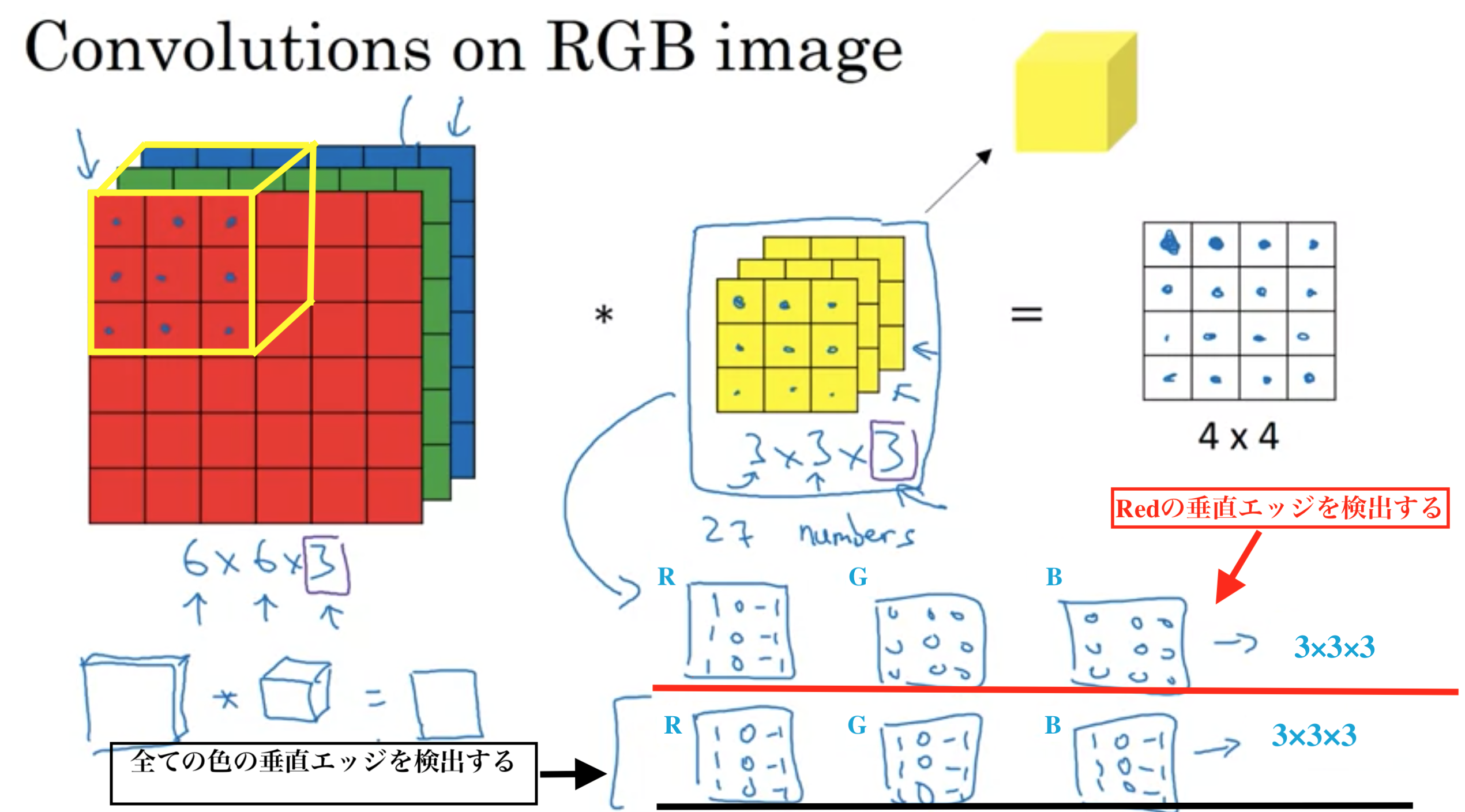 convolutions in RGB image
convolutions in RGB image
垂直エッジだけでなく、水平エッジや30度エッジなど、複数のフィルターを使いたいとき
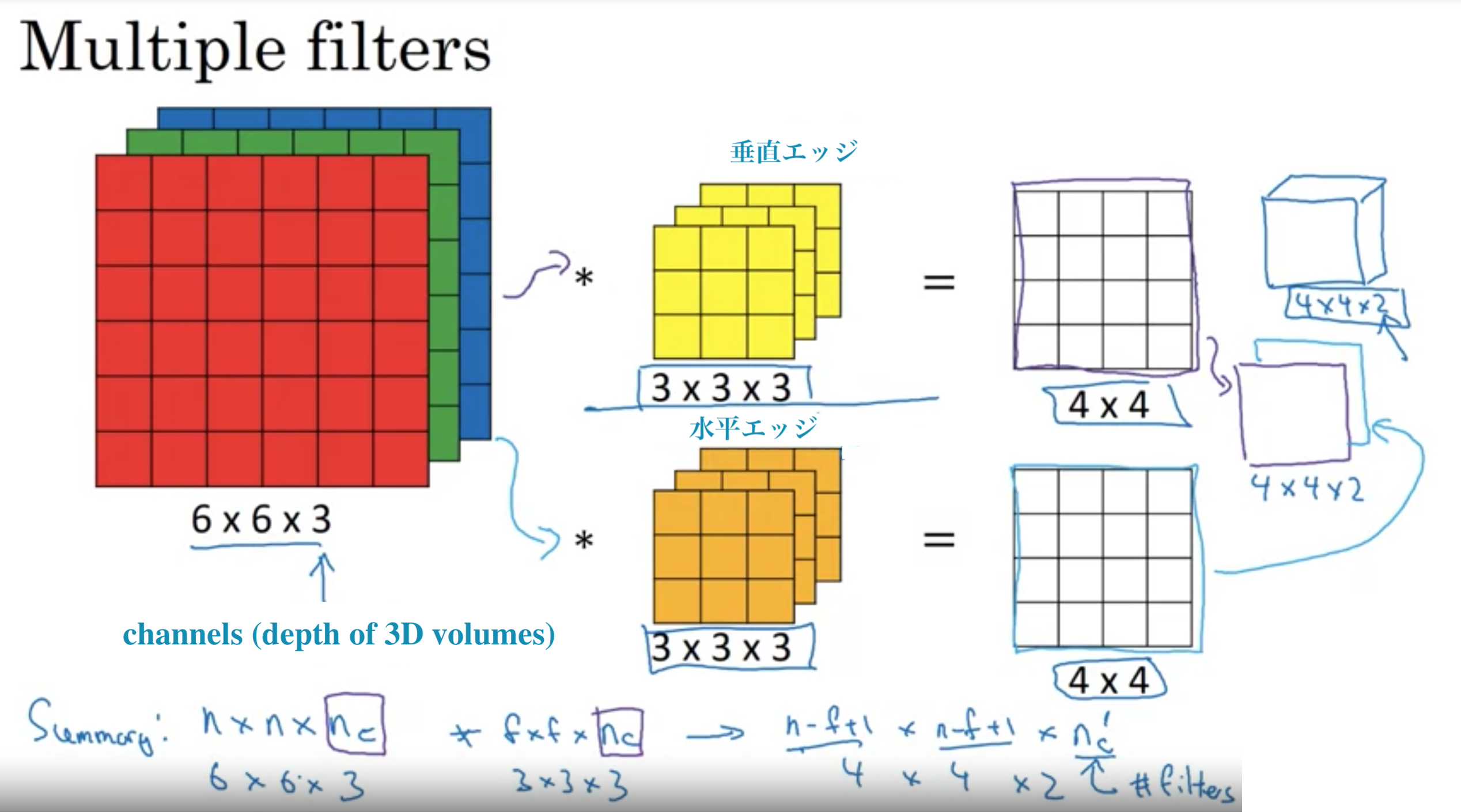 複数のフィルター
複数のフィルター
チャンネル数は文献では、3Dボリュームの深さと表現されたりもする
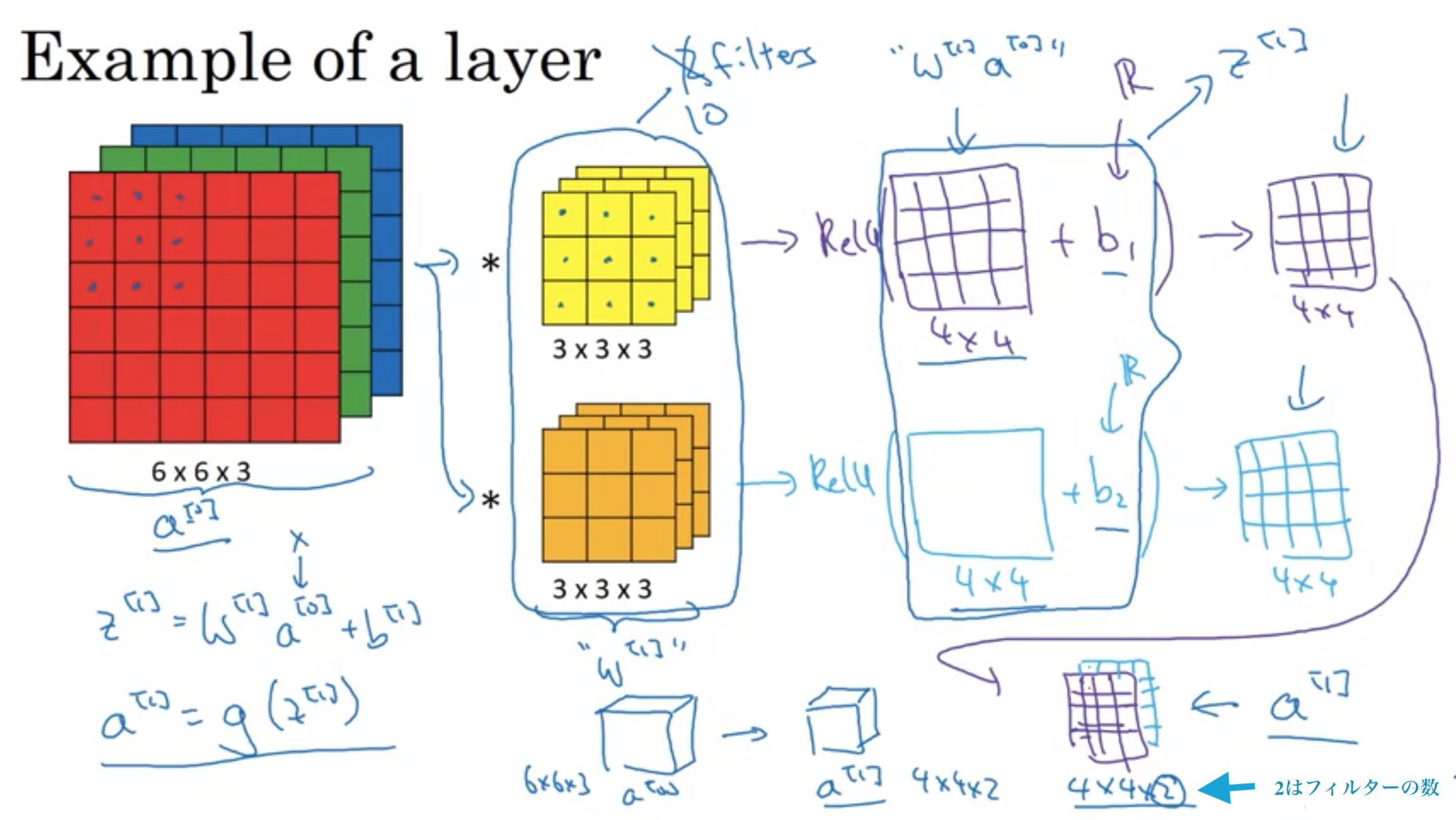 畳み込みニューラルネットワークの一層目
畳み込みニューラルネットワークの一層目
畳み込みニューラルネットワークのパラメータは、フィルターのサイズや次元で決まるので、入力画像がどれだけ大きかろうと、パラメータ数は固定で比較的小さい数になる。
これにより、大きい画像でも訓練ができ、過学習しにくいという特徴もある。
例: 3×3×3のフィルターを10個用いる場合のパラメータ数は?
各フィルターは3×3×3=27でバイアスを合わせることにより合計28このパラメータを有する。合計10個なので、パラメータ数は280個
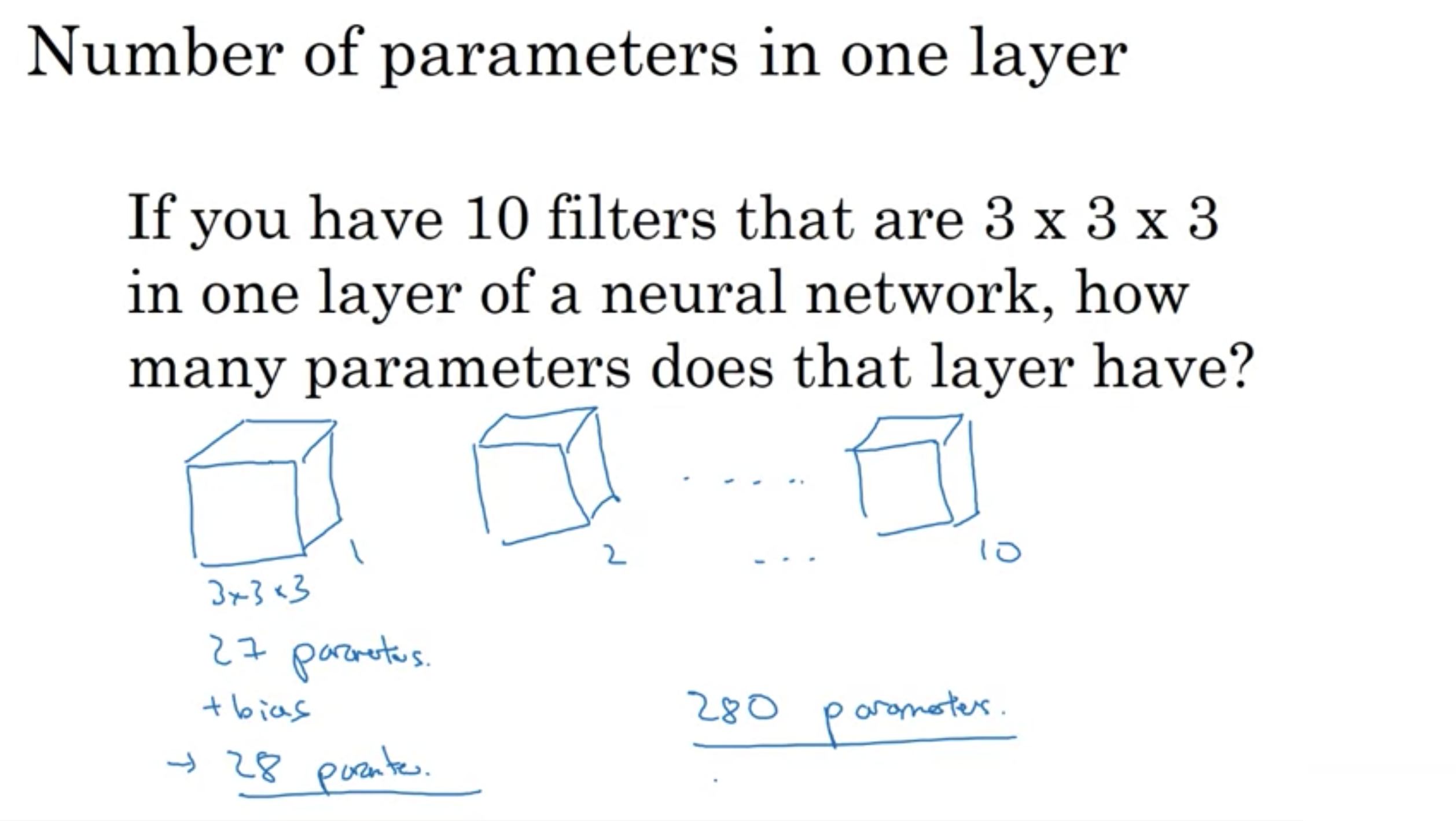 一層目におけるパラメータ数
一層目におけるパラメータ数
畳み込みにおける表現
ただし、高さ×幅×チャンネル数は、チャンネル数×高さ×幅のように、チャンネル数を最初に持ってくることもあれば、最後に持ってくることもあり、規約は統一されていないので、文献によって順番が異なることもある。
l層目が畳み込み層の時:
・\( f ^{ [l] } \) = l層目のフィルターのサイズ
・\( p ^{ [l] } \) l層目のパディング
・\( s ^{ [l] } \) l層目のストライド
・\(n ^{ [l] } _{ C }\) l層目のフィルターの数
・各フィルターは \(f ^{ [l] }\)×\(f ^{ [l] }\)×\(n ^{ [l-1] } _{ C }\)
・活性化 \(a ^{ [l] }\) -> \(n ^{ [l] } _{ H } \) × \(n ^{ [l] } _{ W } \) × \(n ^{ [l] } _{ C }\)
(ミニバッチ数mの時 \(A ^{ [l] }\) -> m×\(n ^{ [l] } _{ H } \) × \(n ^{ [l] } _{ W } \) × \(n ^{ [l] } _{ C }\))
・重み 各フィルター×フィルター数 = \(f ^{ [l] }\)×\(f ^{ [l] }\)×\(n ^{ [l-1] } _{ C }\) × \(n ^{ [l] } _{ C }\)
・バイアス \(n ^{ [l] } _{ C }\) => 実際は4次元行列でshape=(1, 1, 1, \(n ^{ [l] } _{ C }\))
・入力: \(n ^{ [l-1] } _{ H } \) × \(n ^{ [l-1] } _{ W } \) × \(n ^{ [l-1] } _{ C }\)
・出力: \(n ^{ [l] } _{ H } \) × \(n ^{ [l] } _{ W } \) × \(n ^{ [l] } _{ C }\)
・\(n ^{ [l] } _{ H } = \frac{ n ^{ [l-1] } _{ H }+2p^{ [l] }-f^{ [l] } }{ s ^{ [l] } } +1\) (ただし、小数点以下は切り捨て)
・\(n ^{ [l] } _{ W } = \frac{ n ^{ [l-1] } _{ W }+2p^{ [l] }-f^{ [l] } }{ s ^{ [l] } } +1\) (ただし、小数点以下は切り捨て)
 畳み込みにおける表記のまとめ
畳み込みにおける表記のまとめ
畳み込みニューラルネットワーク(Convolutionaal Neural Network) を略してConvNetという
 ConvNetの例
ConvNetの例
畳み込みニューラルネットワークには3つの種類の層がある
日本語では、畳み込み層、プーリング層、全結合層という言い方をする。
convNetは計算を早くして抽出される特徴量を少し堅牢にするために、しばしばプーリング層を使い、表現のサイズを減らす。
最大プーリング: 分割した領域ごとの最大のピクセルを選択 フィルターの中の特徴が高い数を取っておく
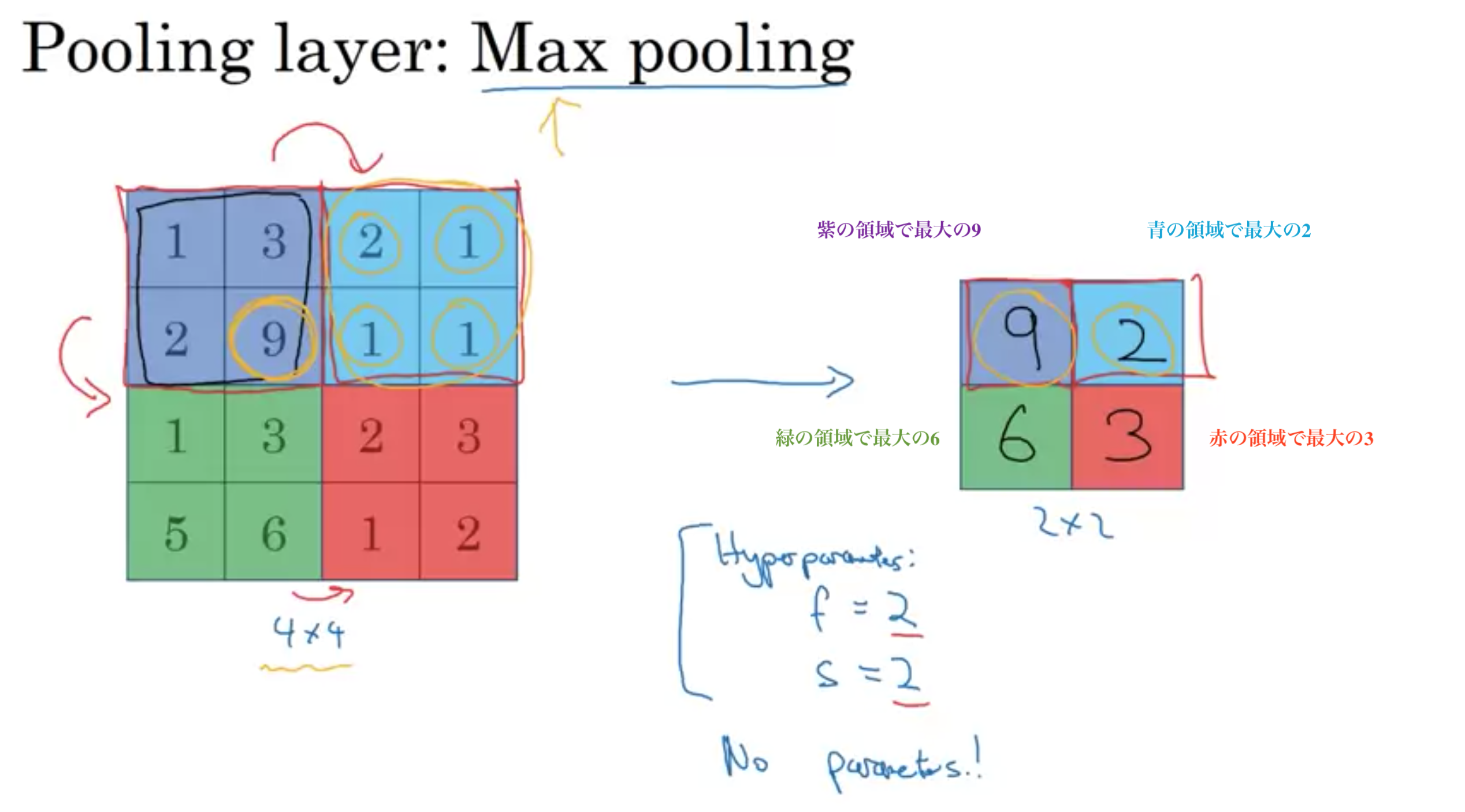 最大プーリングの例1
最大プーリングの例1
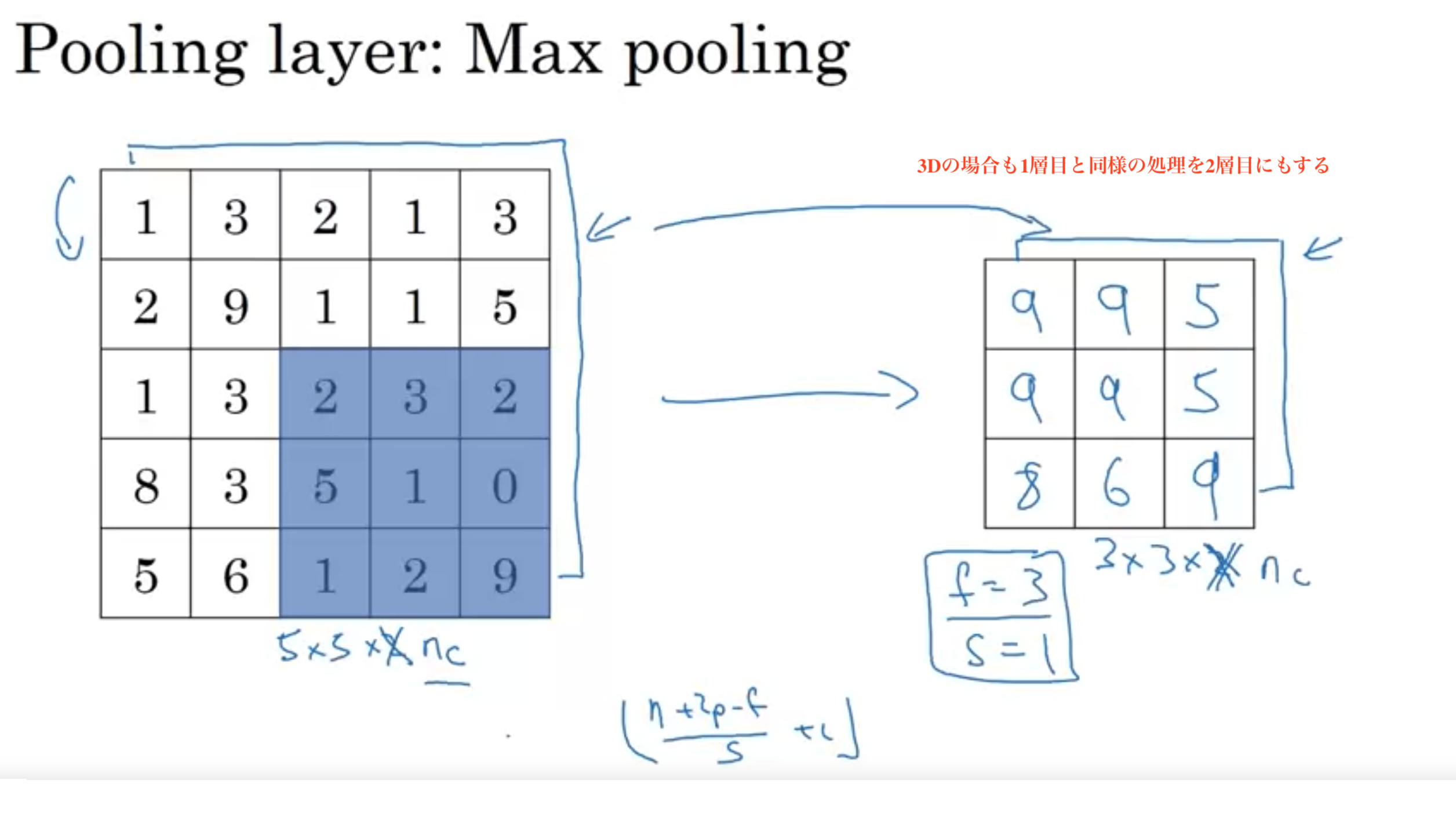 最大プーリングの例2
最大プーリングの例2
平均プーリング: 分割した領域ごとの平均のピクセルをとる
最大プーリングが大変多く使われるため、平均プーリングはあまり使わない。非常に深いニューラルネットワークで、表現を崩すために平均プーリングを使うことがある。
 平均プーリング 例1
平均プーリング 例1
プーリングのまとめ:
最大プーリンングまたは平均プーリング
ハイパーパラメータ:
f: フィルターのサイズ
s: ストライド
ハイパーパラメータのみで、学習するパラメータはない
ハイパーパラメータは手動や、交差検証で設定する
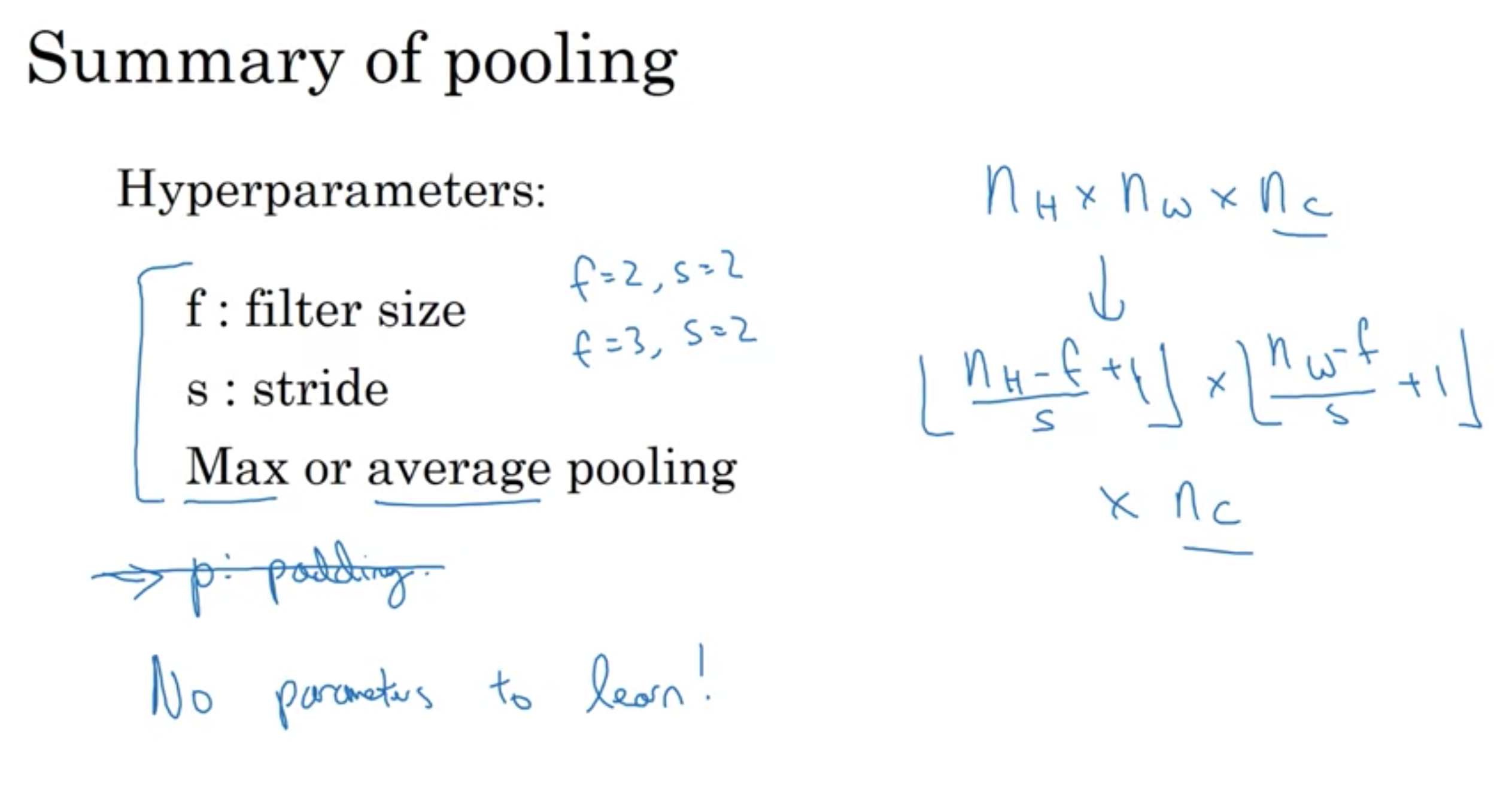 プーリングのまとめ
プーリングのまとめ
文献によっては、畳み込み層とプーリング層をセットで一層とカウントするものもあれば、それぞれを別の層とカウントしたりする。
講師のAndrewさんは、層を数える時、重み(フィルターの行列)を持つ層を数えるので、畳み込み層とプーリング層をセットで1層とカウントする。(プーリング層は、手動で設定するハイパーパラメータのみ)
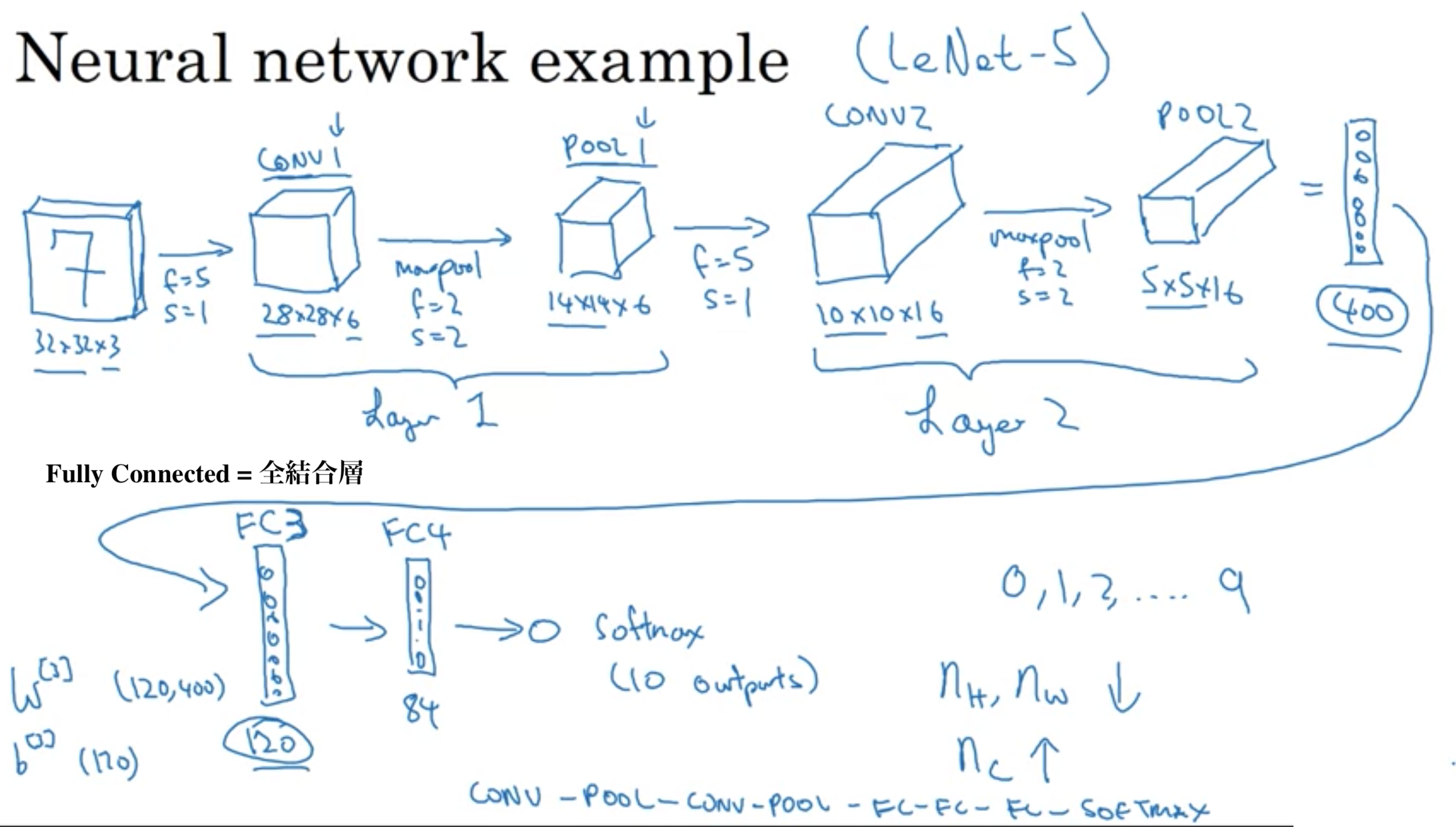 CNNの例1
CNNの例1
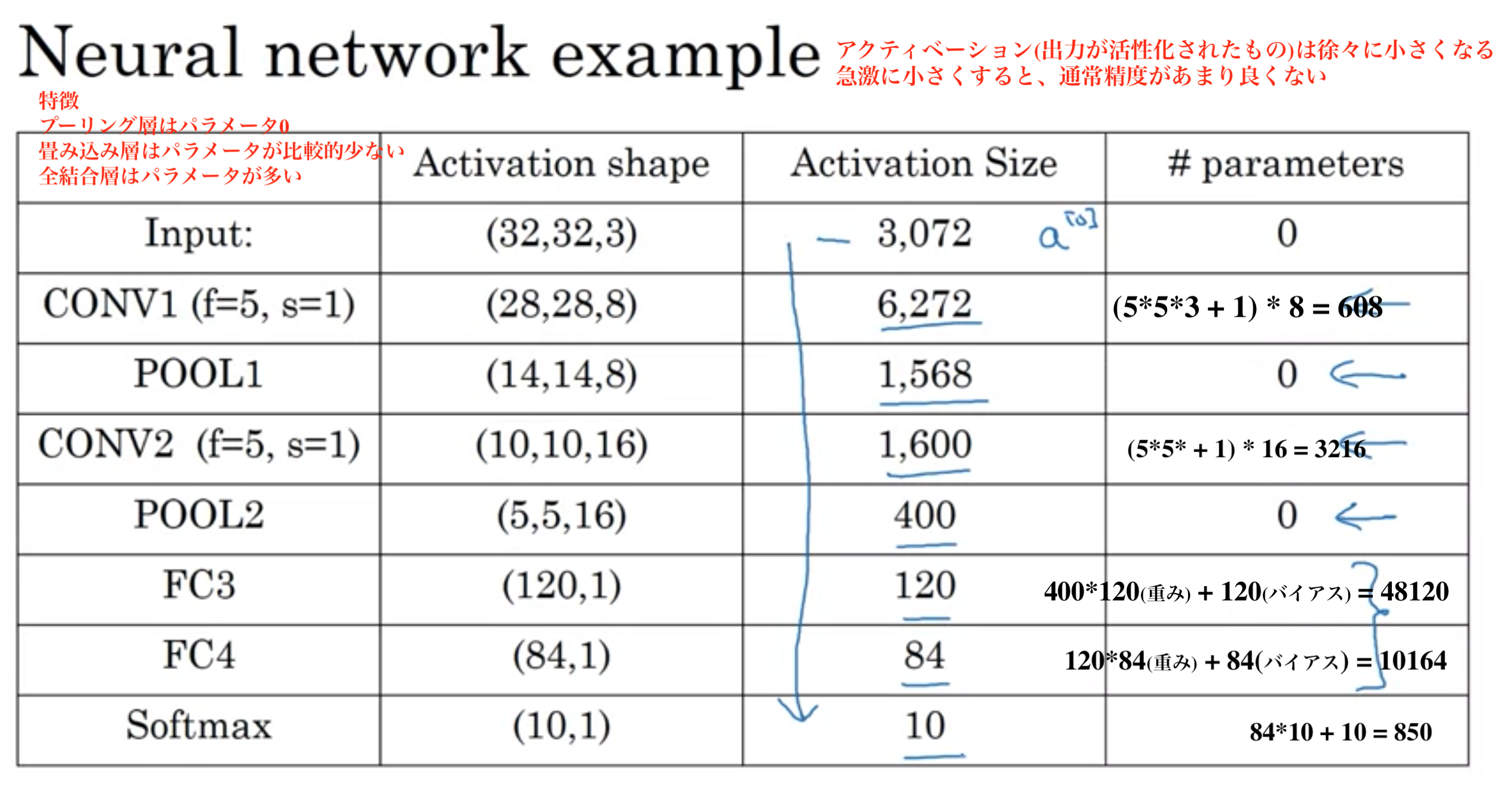 CNNの例2
CNNの例2
全結合層では、各ニューロンにバイアスが1つある。
上記画像ではFC3(全結合層3)では120個のニューロンがあるため、120個のバイアスがある。
なぜ畳み込みをニューラルネットワークに組み込むことが有効なのか?
パラメータの総数を減らし、過学習をしにくくする
特徴検出器を入力画像全体の複数の場所で使用できる (入力画像全体で、どのピクセルを出力する場合でも同じパラメータを扱うことができる)
次のレイヤーの各アクティベーションは、前のレイヤーの少範囲のアクティベーションにのみ依存する
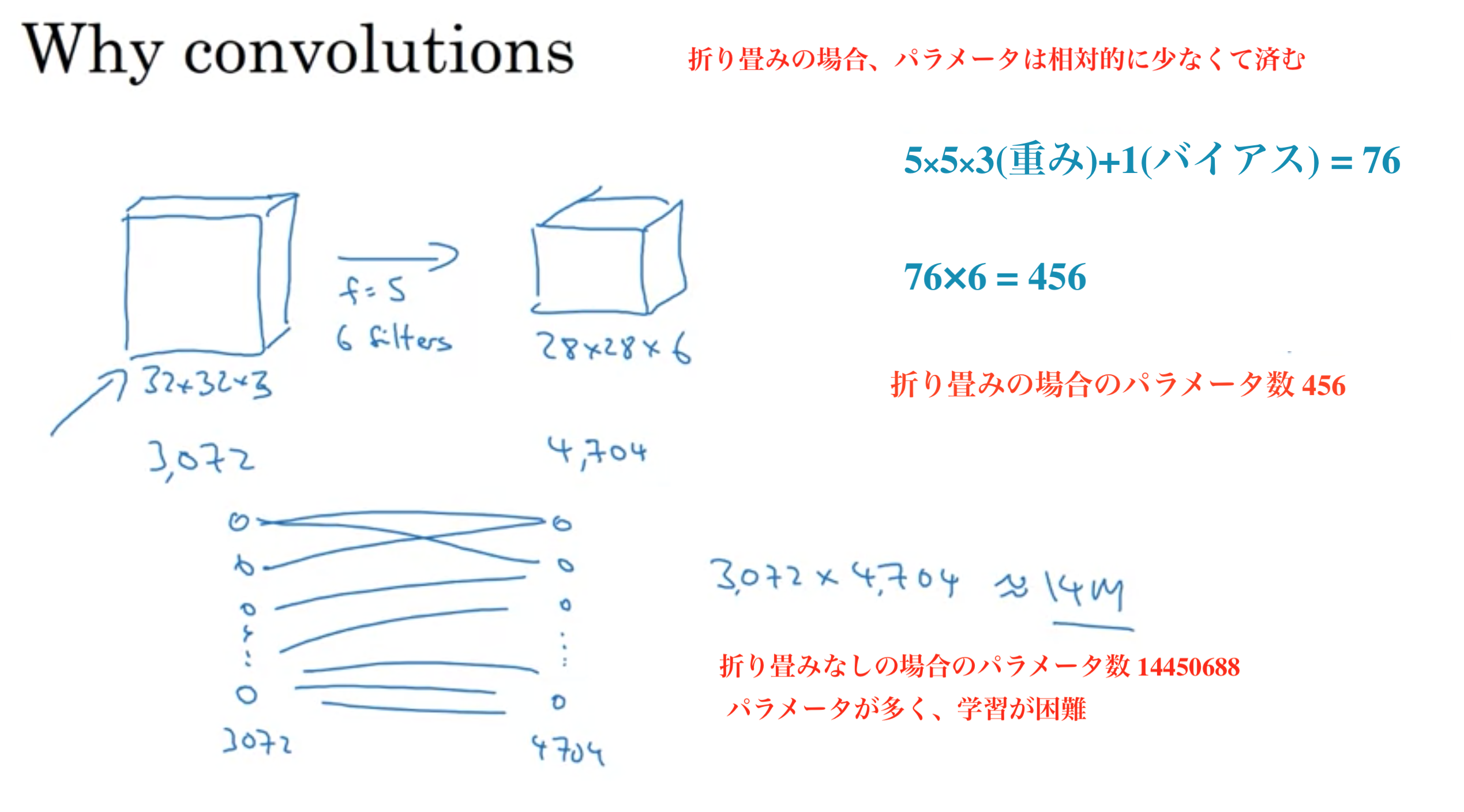 CNNのパラメータ比較
CNNのパラメータ比較
・パラメータ共有
畳み込みは、ストライドでずらしながら同じパラメータを入力画像の多くの異なる位置で使用する。
・結合のスパース化(疎)
入力画像をフィルターで畳み込みする時、出力の各ピクセルは、フィルターの適用範囲のみに依存し、範囲外のピクセルの影響を受けない。
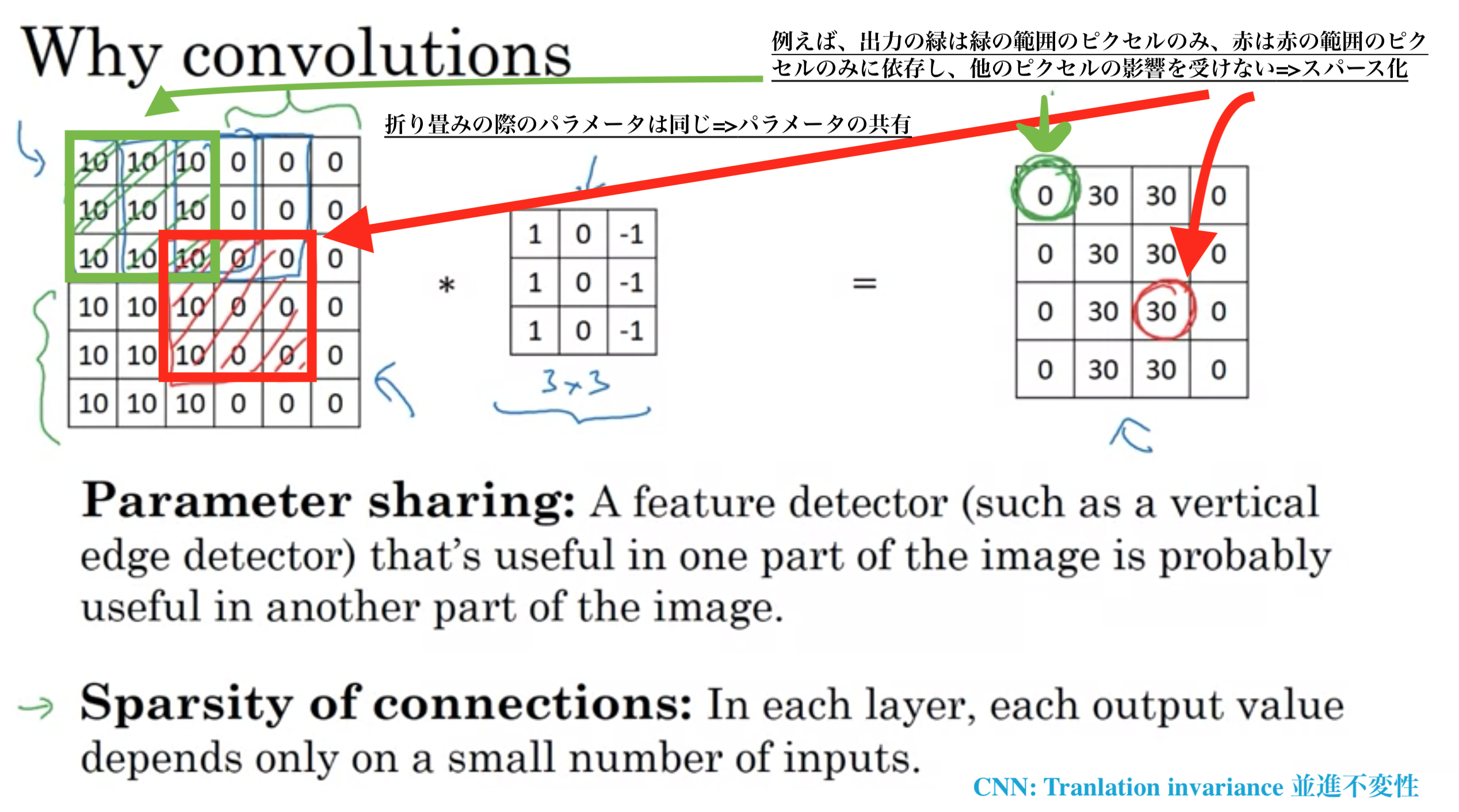 CNNのパラメータが比較的少ない理由
CNNのパラメータが比較的少ない理由
CNNは並進不変性を得るのに非常に良い
並進不変性とは例えば、猫の絵を少し並進移動しても、それはまだ猫の絵として認識できる性質のこと。
参考記事
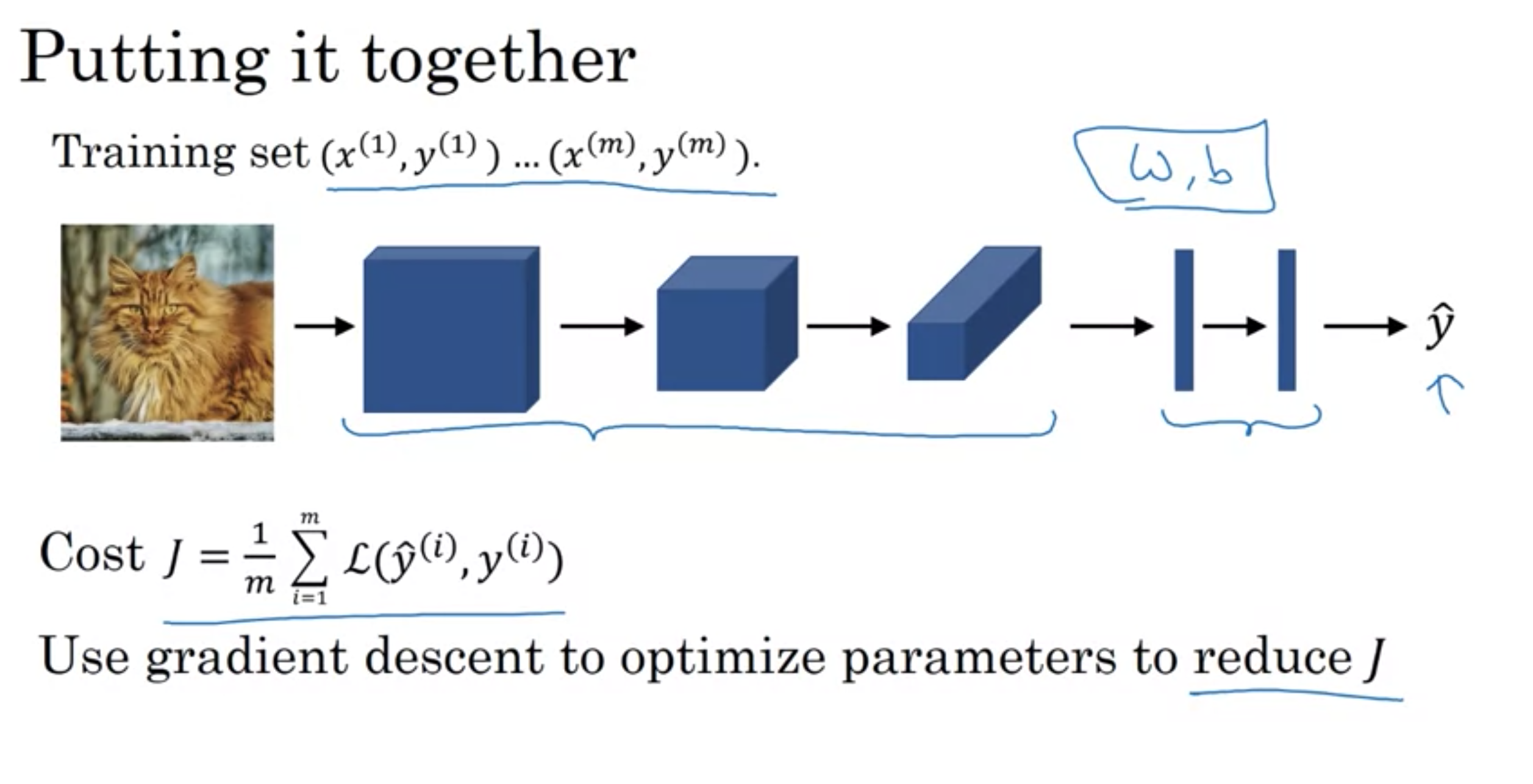 CNNの学習
CNNの学習
講義では、CNNの誤差逆伝播の話が出てこなかったが、課題では逆伝播の内容も出題されていた。
CNNの逆伝播は非常に記事が少なく、難しい式だけで説明が終わっているものがほとんど。
以下は筆者が自主的に調べて例を例をあげたものである。
なお、講義では説明のない部分であるため、別にスキップしても構わない。
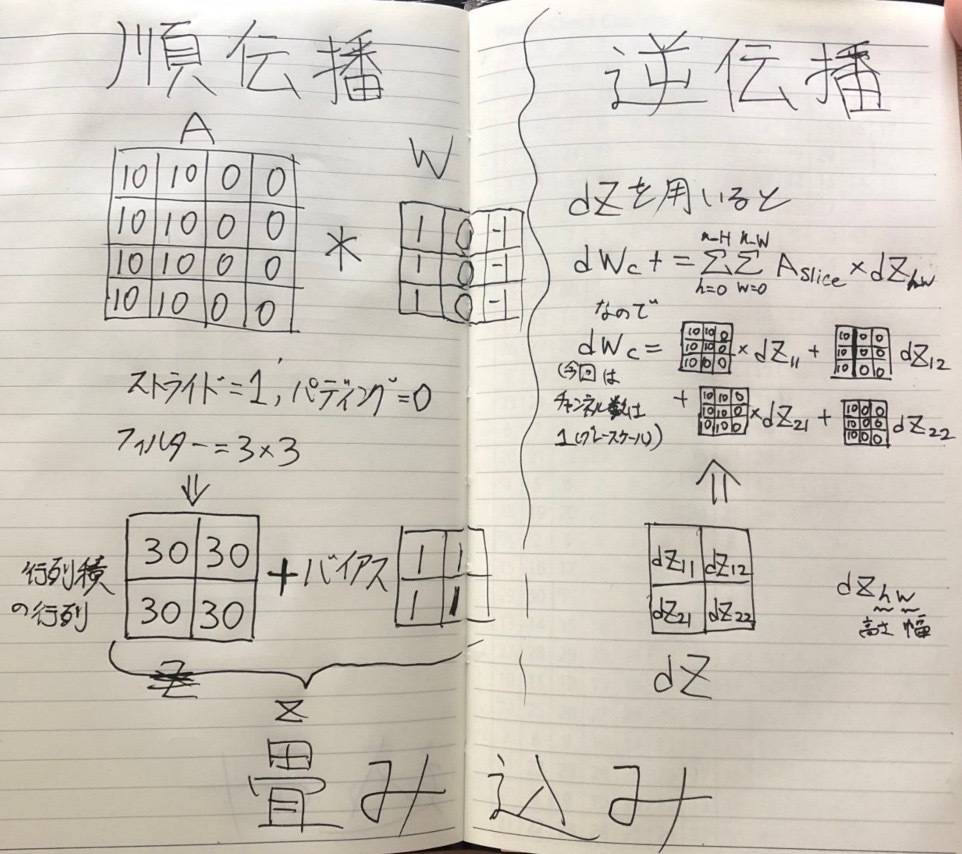
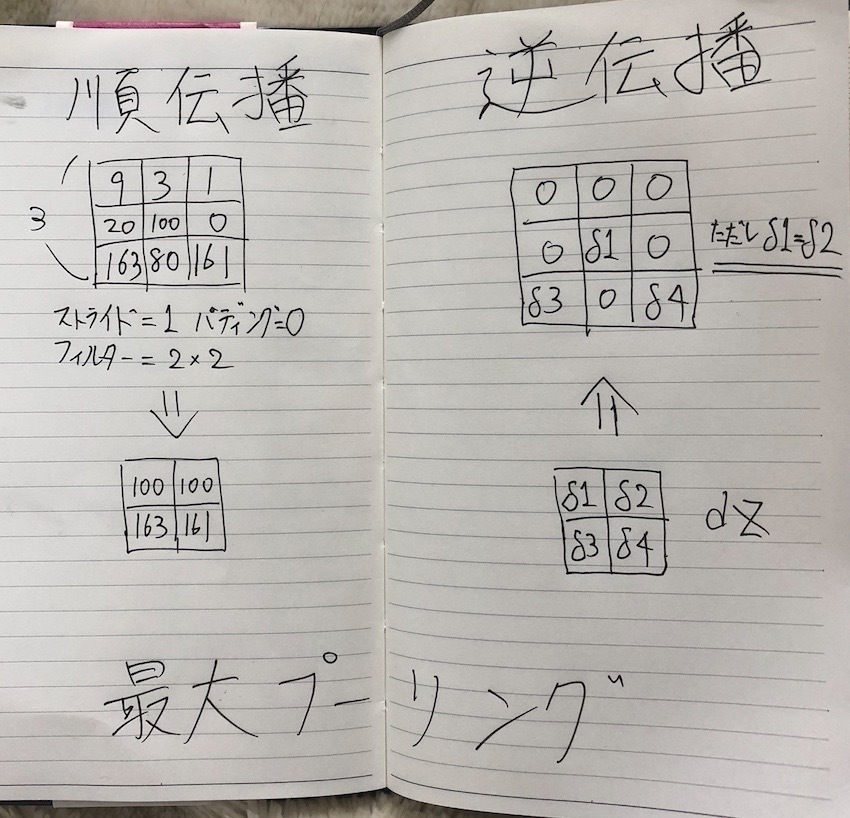 最大プーリングの順伝播と逆伝播
最大プーリングの順伝播と逆伝播
 平均プーリングの順伝播と逆伝播
平均プーリングの順伝播と逆伝播
*古典の意味: 古い書物、形式。 また、長く時代を超えて規範とすべきもの
古典的なネットワーク
ResNet (152層)
Inception
・1998年にYann LeCunさんが発表した
・グレースケールで学習する (Lenet-5は手書き文字の認識のために作られたため)
・畳み込みを行うたびに画像が縮んだ (当時は、パディング の概念がなく、まだValid Convolutionのみの時代であった)
・層が進むに従って画像の幅、高さが縮む一方で、チャンネル数は増加する
・1つ以上の畳み込み層を置き、次にプーリング層を置く。そして、1つ以上の全結合層を置き、出力を得る (今日でも非常に良く使われるパターン)
・2020年現在は、出力層でソフトマックス関数を使うが、当時は出力層に異なる分類器を使っていた (今日では役に立たないもの)
・約6万個のパラメータを持っている (今日では1千万から1億のパラメータを持つこともしばしばなので、それほど多くはない)
発展:
・sigmoidとtanhで非線形化していた (当時はReLuは使っていなかった)
・プーリング層の後に非線形化していた
 古典的なネットワーク LeNet-5
古典的なネットワーク LeNet-5
・コンピュータビジョン界で衝撃を与え、ディープラーニングが真剣に使えると人々を信じさせたきっかけの論文
・LeNet-5と似ているが、はるかに大きなネットワーク
・6千万個のパラメータがある
・複数のGPU
・局所応答正規化 (目的は、非常に高く活性化するニューロンを数多くは欲しくないから)
(例えば、2層目のプーリング層の出力は高さ、幅、チャンネル=13×13×256であるが、局所応答正規化 をするときは、13×13の画像の各場所で、1×1×256のブロックごとに256個を正規化する)
局所応答正規化は、あとで多くの研究者によってそれほど助けにはならないことがわかった。つまり、今日では必要ない。
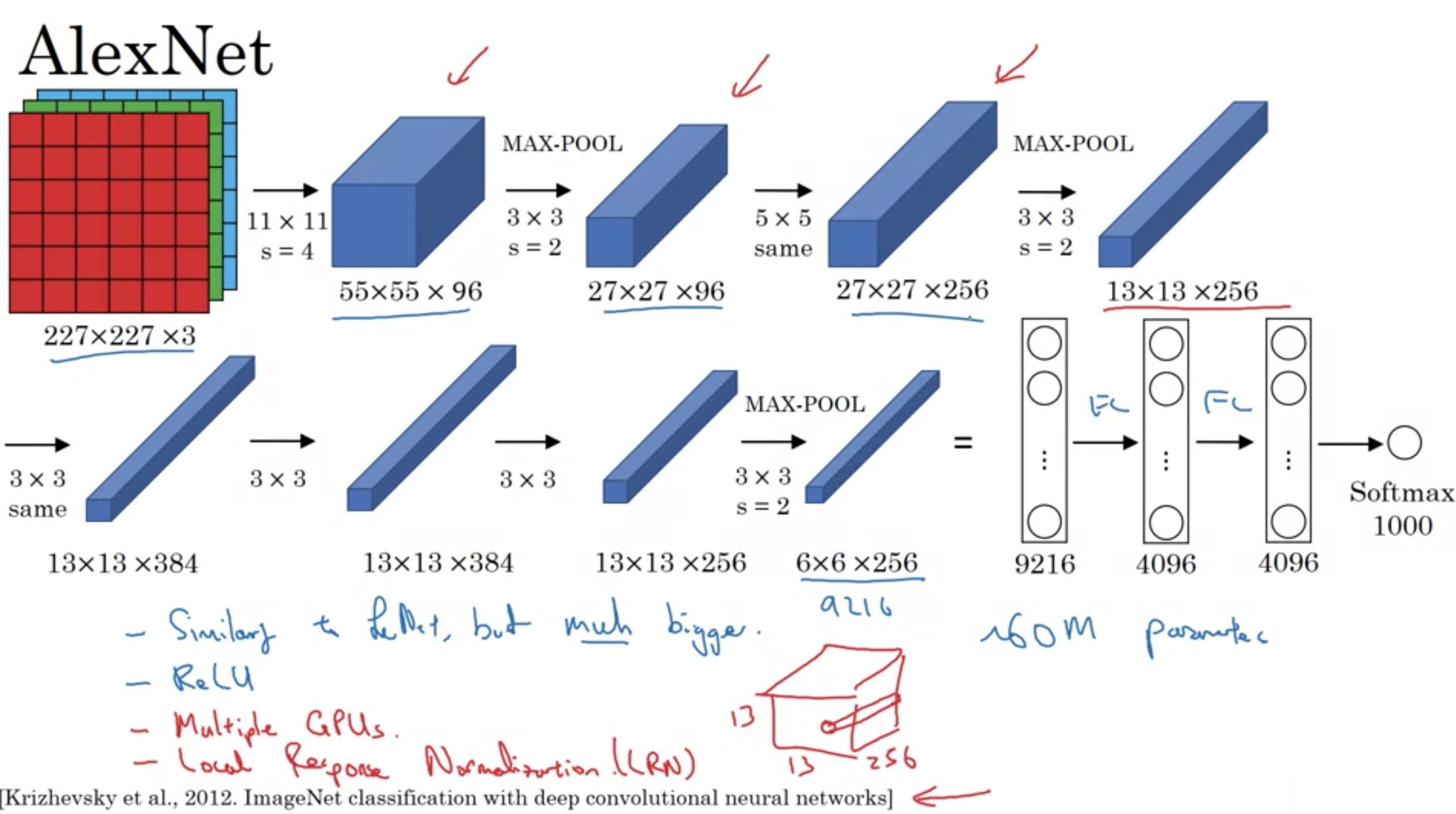 古典的なネットワーク AlexNet
古典的なネットワーク AlexNet
・VGG-16の16は、重みを持つ層が16個あることに由来する
・1億3千8百万個のパラメータを持つ (現在の基準から見てもかなり多い)
・多くのハイパーパラメータを持つ代わりに、ストライドが3 x 3のフィルターであるconv-layersのみを使用することに重点を置いた、はるかに単純なネットワークを使用
・使用する畳み込みは全てConv=3×3フィルター, s=1, same convolution、使用するプーリングは全て最大プーリング MAX-POOL=2×2, s=2
・良いところは、ニューラルネットワークの構造を単純にすること
・欠点は非常に多くのパラメータを持つとても大きなニューラルネットワークを学習させなければならないこと
・畳み込みを行うたびにチャンネル数を倍にする (64->128->256->512 ただし、512は十分に大きいので、著者は512からさらに増やすことはしなかった)
文献では時々、VGG-19を目にする。VGG-16とほとんど同じだが、サイズが少し大きい。
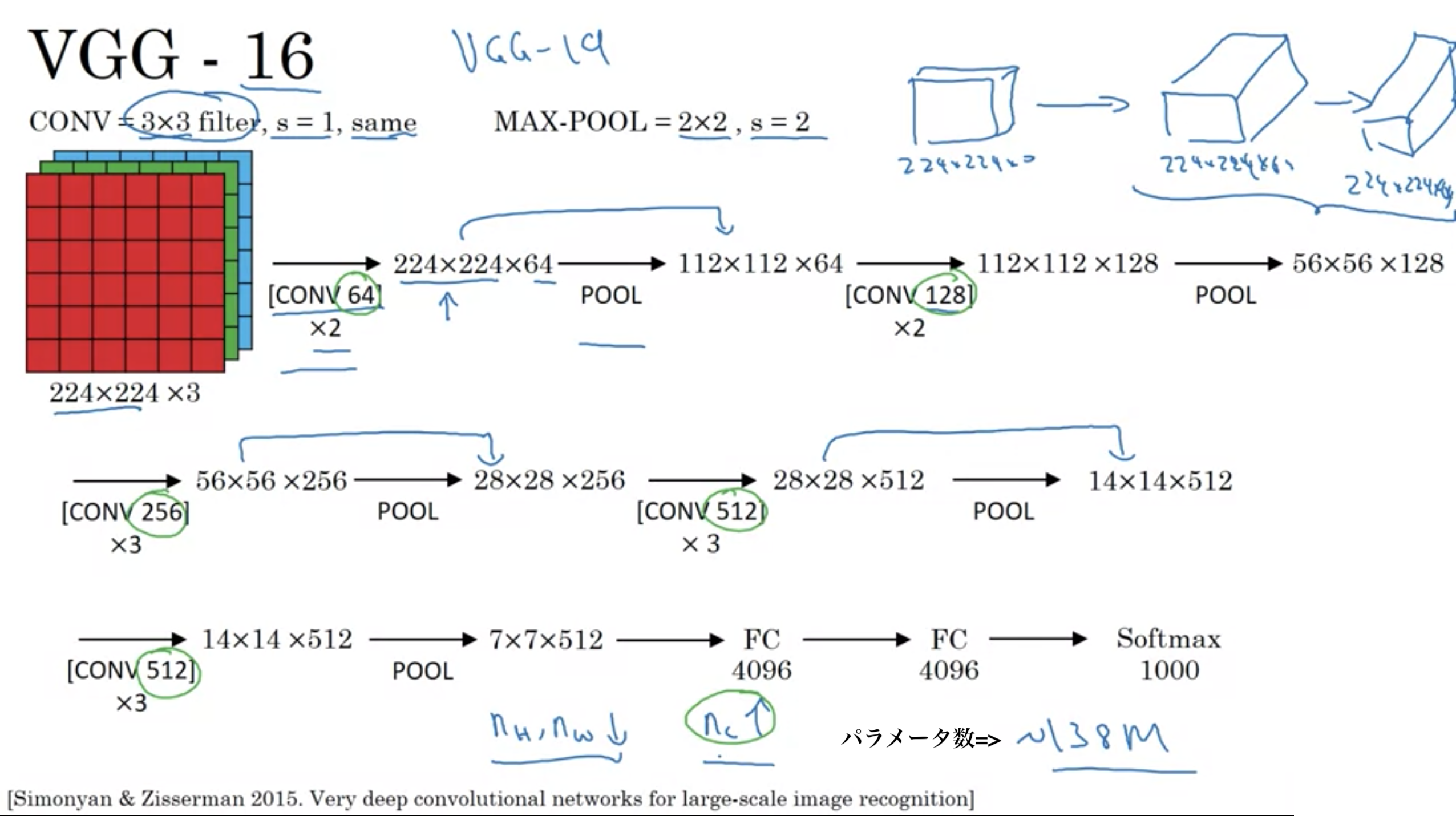 古典的なネットワーク VGG-16
古典的なネットワーク VGG-16
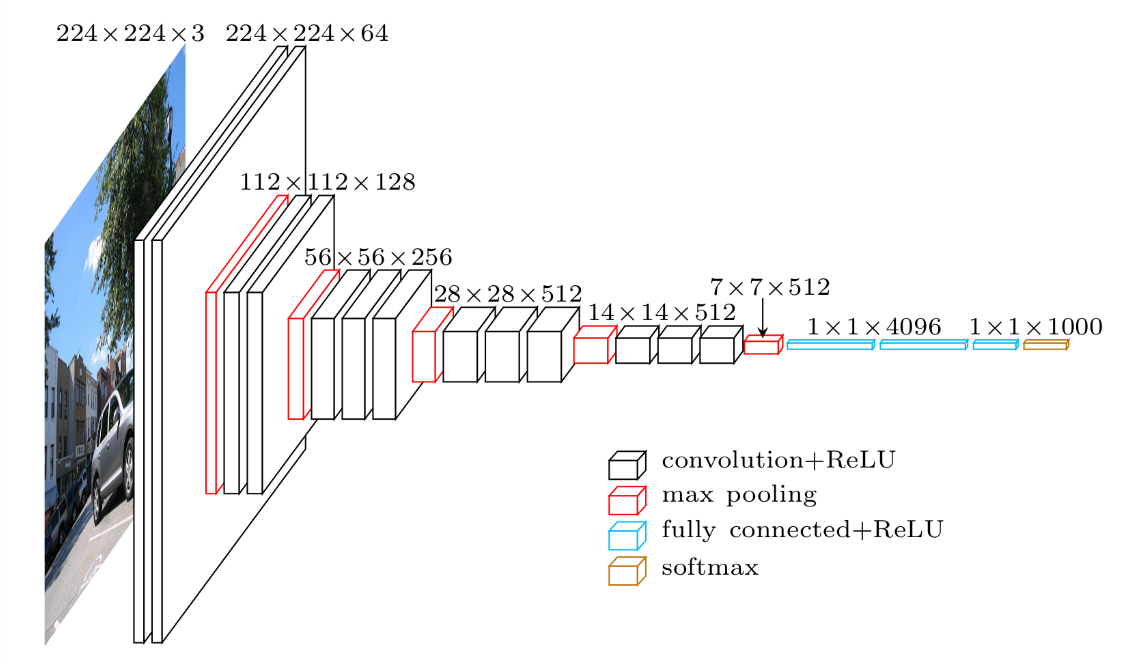 VGG-16 モデルイメージ
VGG-16 モデルイメージ
プーリング層は学習するパラメータが存在しないので、層にはカウントしない。
VGG-16は16層からなる。
ResNetは残差(Ressidual)ブロックを使うことで、より深いネットワークの学習を可能にする
ResNetは、スキップコネクションのおかげで、深い層でも学習が可能
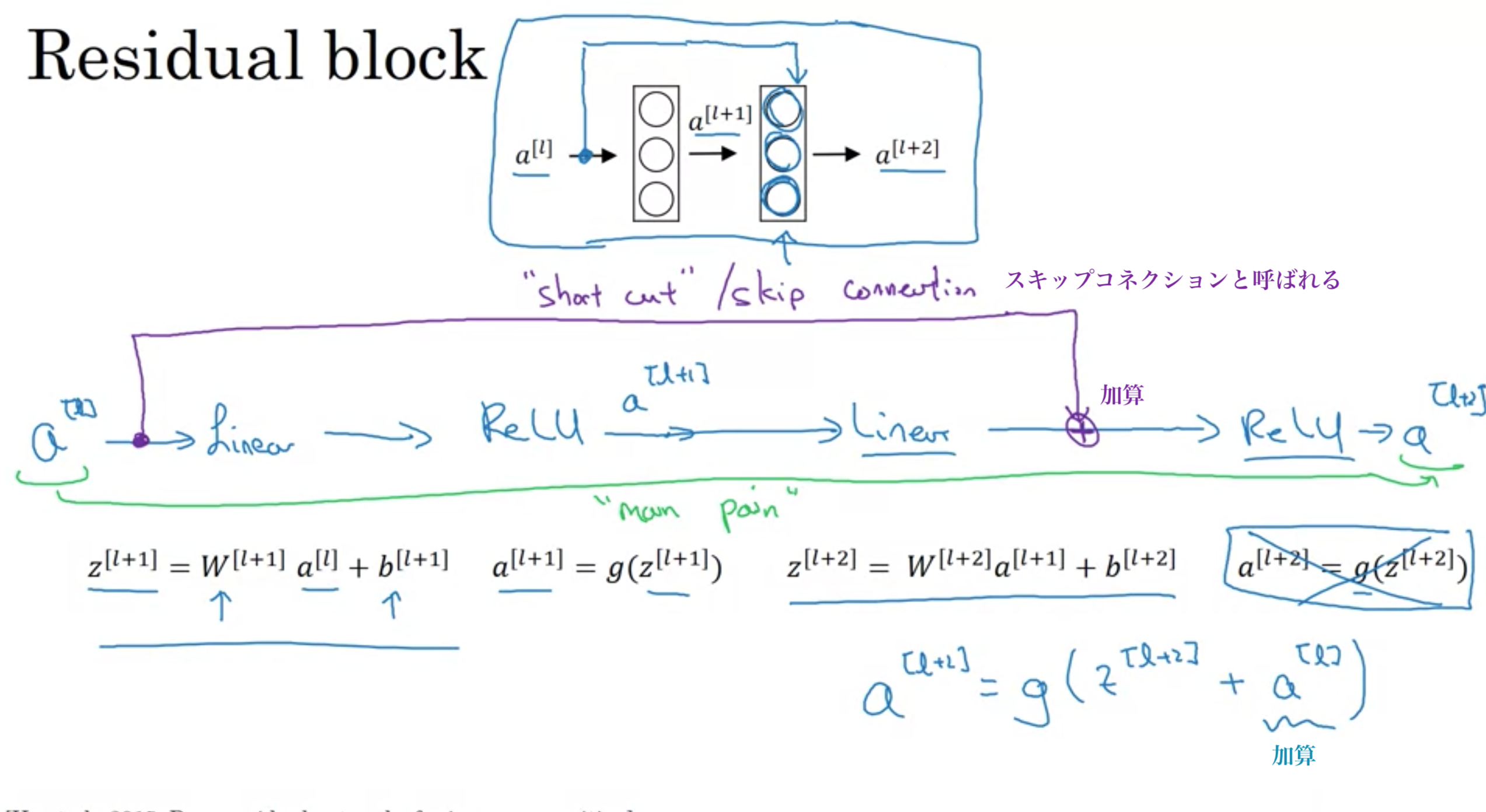 ResNet (Redidual Neural Network)
ResNet (Redidual Neural Network)
・スキップコネクションによる残差ブロックがない、標準的なニューラルネットワークの場合
層が深くなるほど、訓練誤差はしばらく減った後に、また増え始める傾向がある
理論的には、層が増えれば増えるほど学習セットに対してどんどん良くなっていくはずだが、実際は、深い標準的なネットワーク(ResNetでない)では最適化アルゴリズムによる学習は難しく、あまり深すぎると学習誤差は増加する。
・ResNetの場合
層が深くなるほど、訓練誤差はしばらく減った後に、平らになる。
とても深いネットワークの学習を助ける。
層が深くなっても(たとえ、100層で訓練したとしても)、訓練誤差を下げ続けるような性能を得ることができる。
ResNetは層を深くしても、少なくとも訓練セットでは性能を損なわない。
スキップコネクションにより、重みやバイアスが0になると、 \(a ^{ [l+2] } = g(z^{ [l+2] }+a^{ [l] }) = g(w^{ [l+2] }a^{ [l+1] }+b^{ [l+2] }+a^{ [l] }) = g(a^{ [l] })= a^{ [l] } \)となるため、残差ブロックは恒等関数を容易に学習する
これが意味することは、l+1, l+2層目の2層をニューラルネットワークに加えることは、ニューラルネットワークの性能を一切損ねない。
残差がないニューラルネットワークでは、層を深くしていくと、パラメータを選択するのが難しくなる。(恒等関数を学習することさえも難しい)
・ResNetがうまく機能する一番の理由は、間の2層が容易に恒等関数を学ぶので、性能を損ねないよいう保証があるため。
・l層目とl+2層目は次元を同じにする \(g(z^{ [l+2] }+a^{ [l] })\)を計算可能にするため
\(z^{ [l+2]}\)の次元が256、\(a^{ [l]}\)の次元が128の時、次元を揃える手段は2つ(どちらもうまくいく)
1. \(R ^{ 256×128 }\)の変数\(w _{s}\)を\(a ^{l}\)に掛けて、256次元にする (\(w _{s}\)を学習可能なパラメータにする)
2. \(a _{l}\)をゼロパディングして次元を256に合わせる
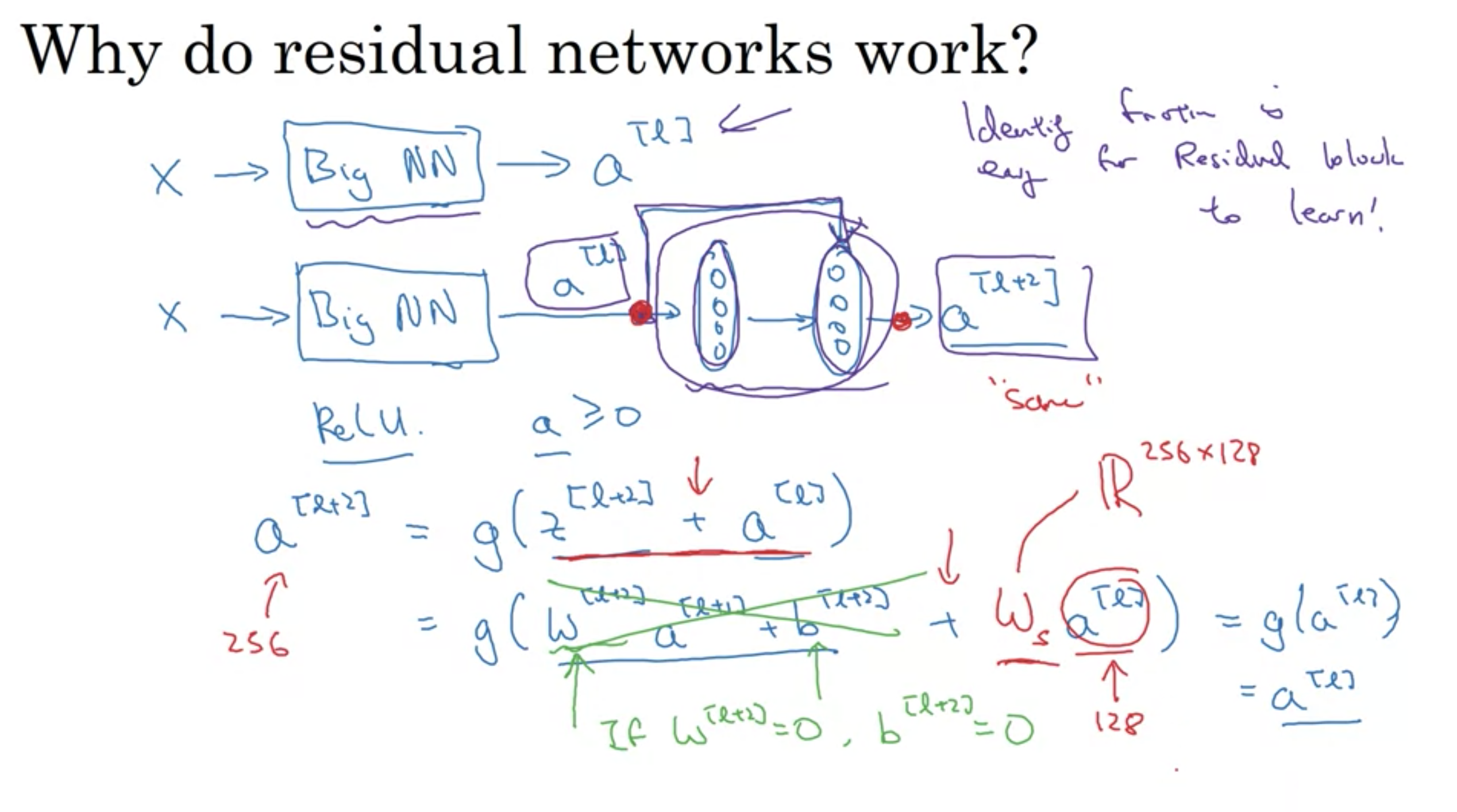 ResNetが深い層でも訓練誤差が増えない理由
ResNetが深い層でも訓練誤差が増えない理由
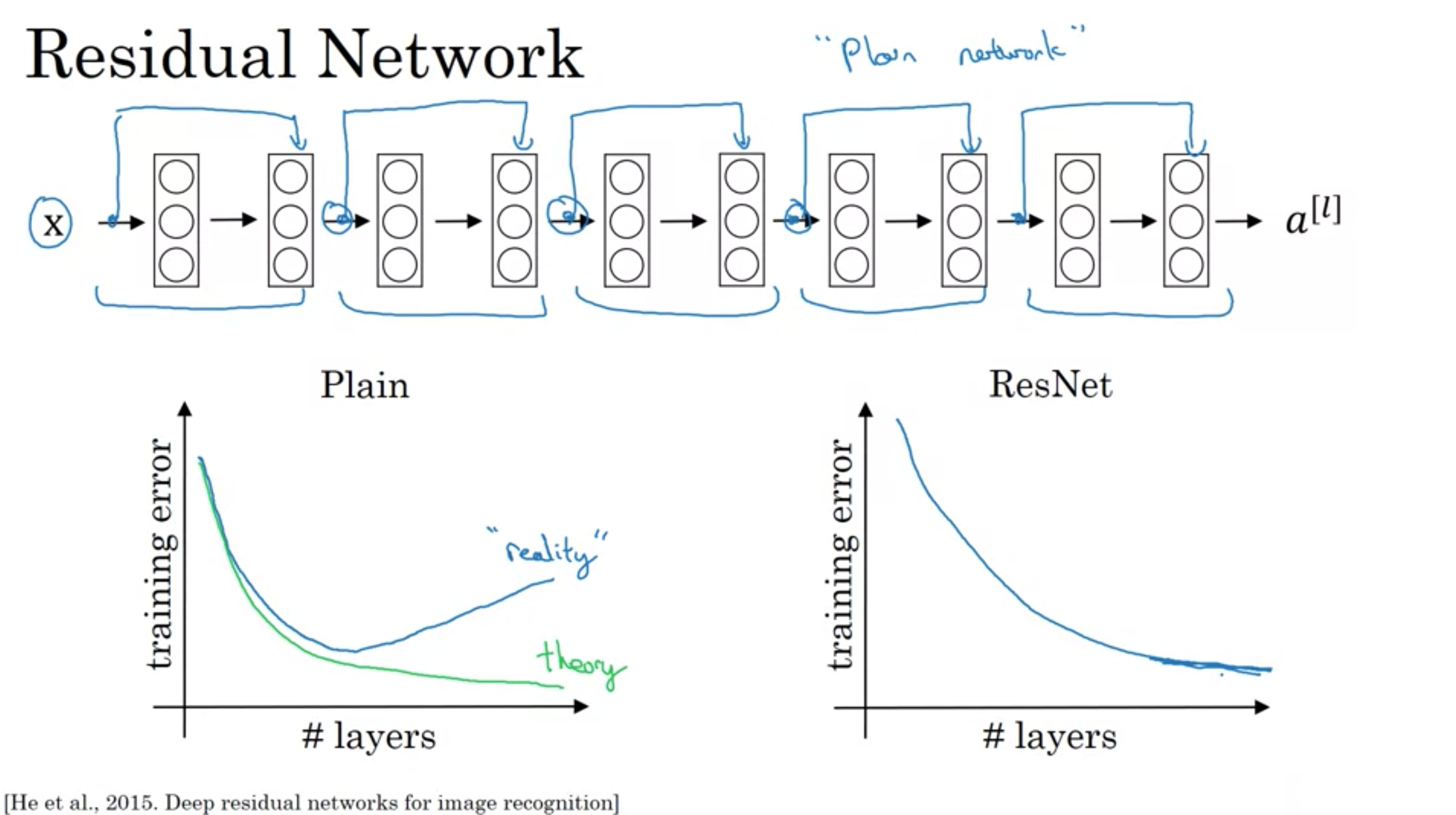 ResNet vs plain network
ResNet vs plain network
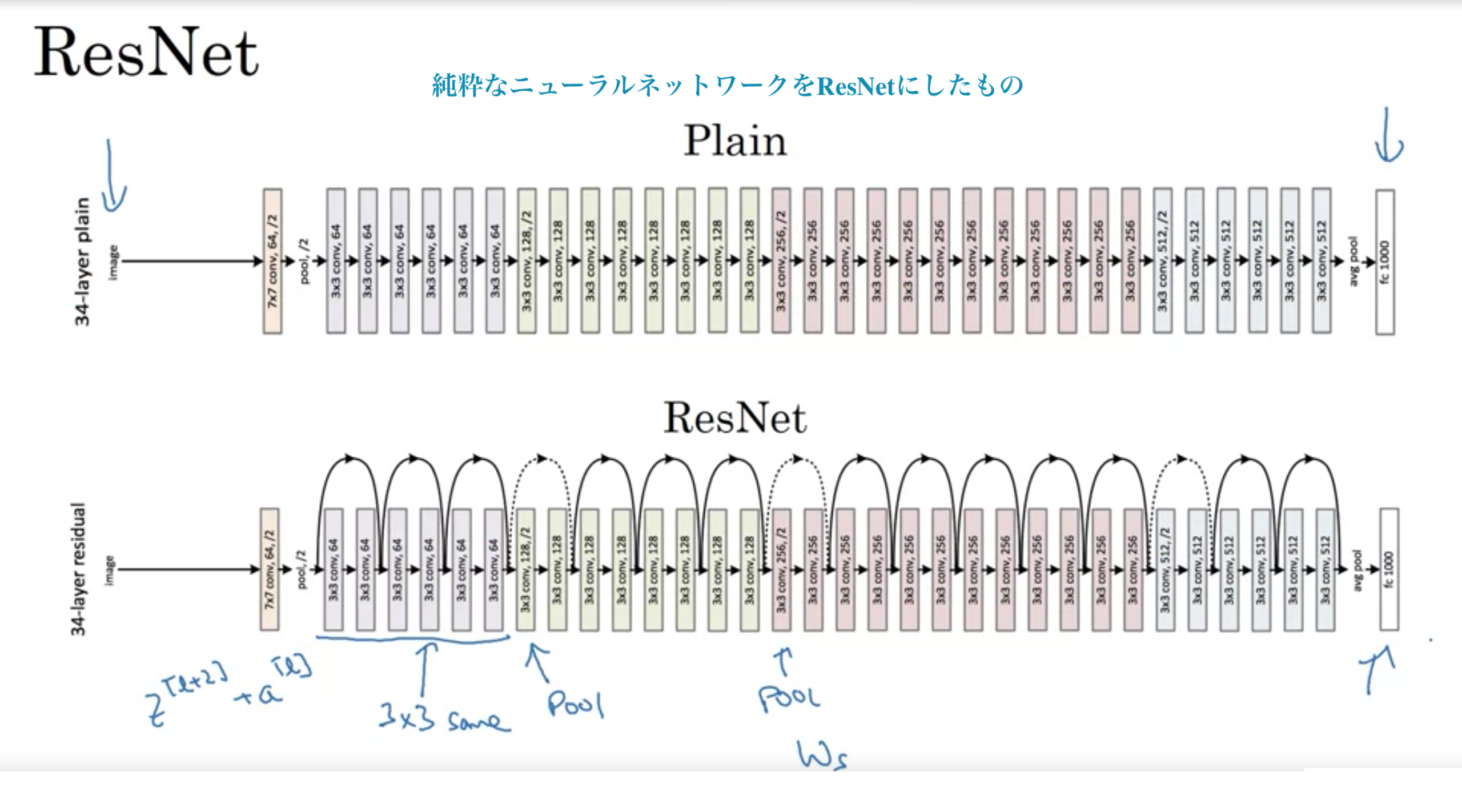 ResNet
ResNet
[He et at., 2015 Deep Residual Networks for image recognization]
入力が6×6×1の場合、フィルター1×1、値2で畳み込むと、単にピクセルを2倍するだけでは...チャンネル数が1だったから意味がない。
入力が6×6×32の場合、フィルター1×1×32を使って畳み込むと、ニューロン32個を使って、ピクセルを出力するのと同じ。
出力は6×6×<フィルター数>になる。フィルターの数を調整することによって、出力のチャンネル数を減らしたり、増やしたり、一定に保ったりできる。
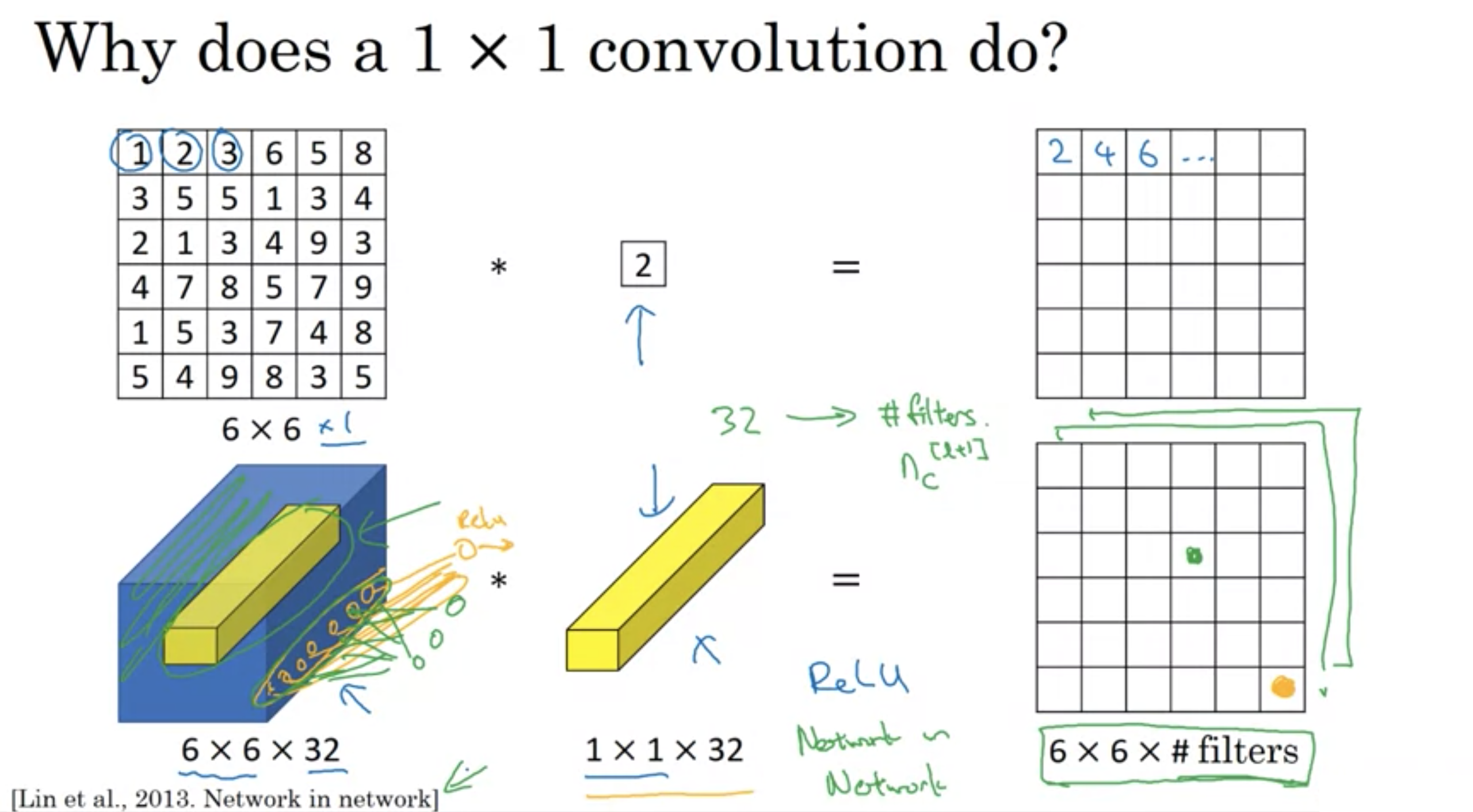 1×1畳み込みの役割
1×1畳み込みの役割
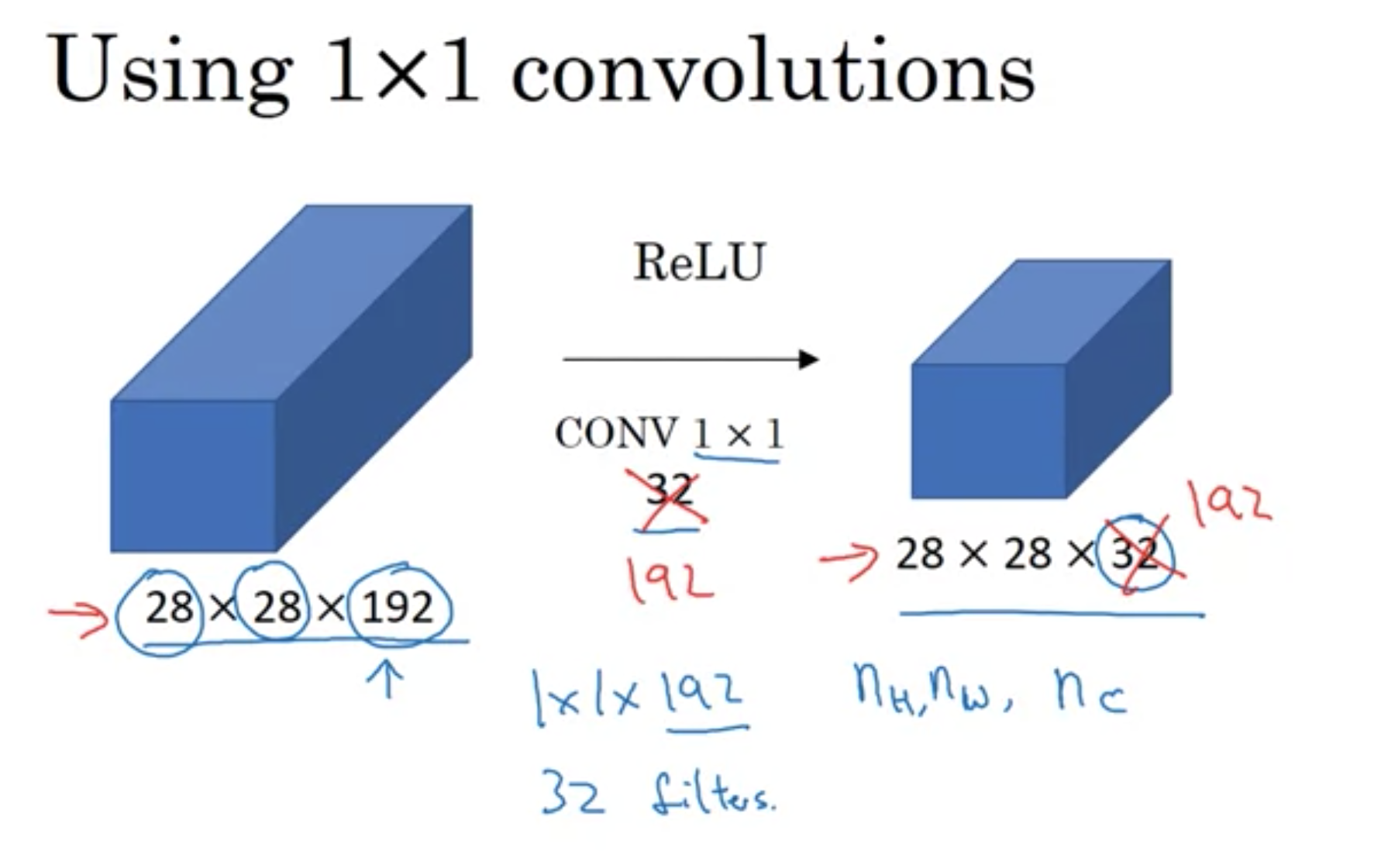 1×1畳み込みの使用
1×1畳み込みの使用
畳み込み層を設計する時、以下を選ばなければならない。
フィルターのサイズをどうするか? (1×3、3×3、5×5など)
プーリング層を入れたいか?
Inceptionネットワークは全てできる。
全てを行い、全ての出力をチャンネル数を軸として結合する。ただし、出力画像の幅、高さを同じにする
 inception network
inception network
しかし、コストを計算するときに、計算量が膨大になる。
以下のスライドでは、コストの計算の際にかけ算を行う回数が1億2千万回に相当する
現在のコンピュータなら実行できるが、それでも高くつく。
そこで...1×1のフィルターを挟み、サイズを縮小させる。
今回のケースでは、計算コストを1/10ぐらいまで減らすことができる。
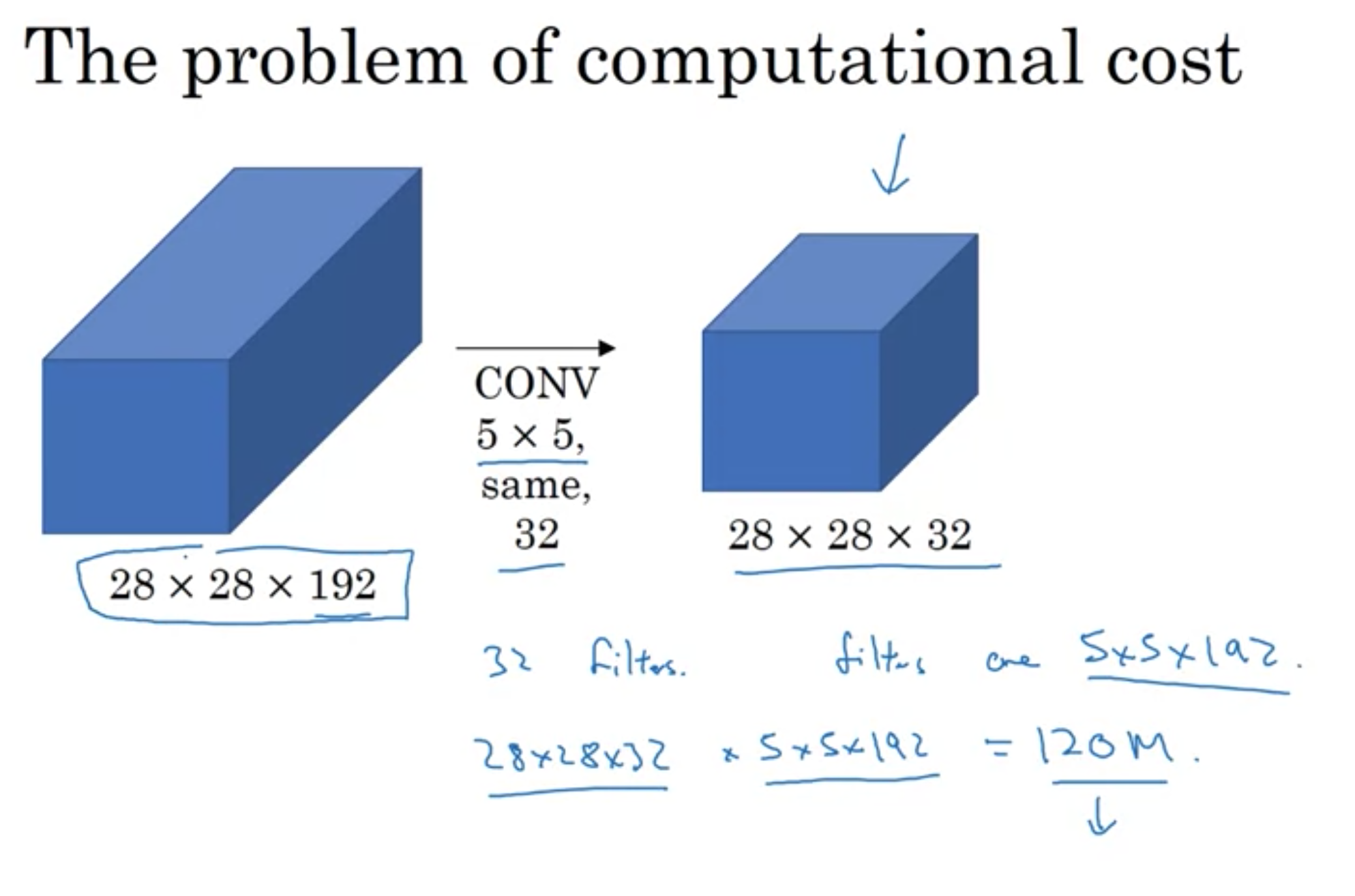 inception netowork コストの問題
inception netowork コストの問題
1×1フィルターを中間層として挟むことで、ボリュームを縮小させてコストの計算量を減らす。
挟む1×1フィルターをボトルネック層と呼ぶ。(ボトルネックとは通常何か一番小さい部分を表す)
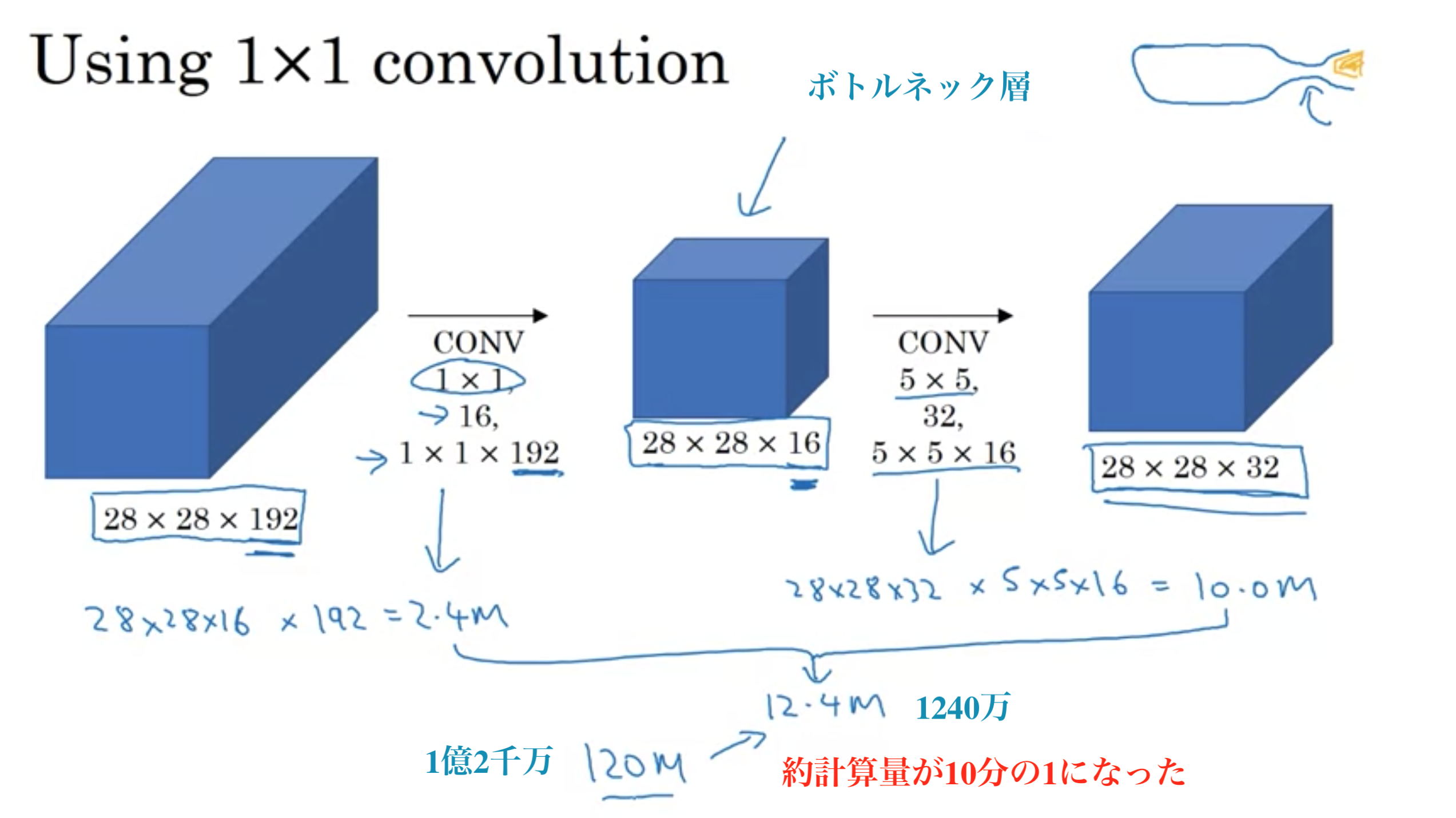 1×1畳み込みの使用 (ボトルネック層の挿入)
1×1畳み込みの使用 (ボトルネック層の挿入)
表現のサイズを劇的に縮めてネットワークの性能を損ねないのか?
コストの計算量を減らす目的においては、ボトルネック層を実装する限りにおいては、表現のサイズを極端に減らすことができ、性能を損ねないことがわかっている。
まとめ
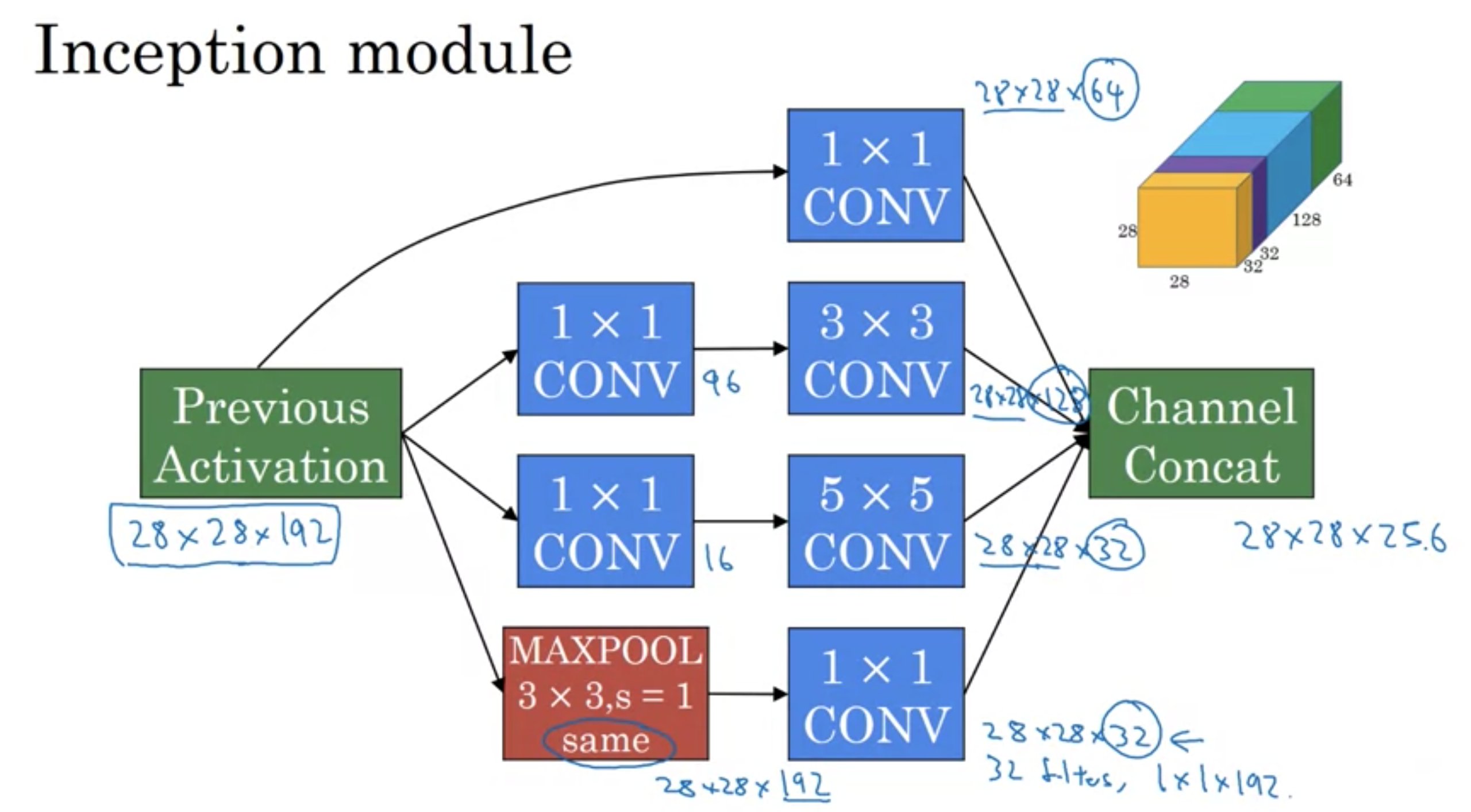 Inception moduleの一例
Inception moduleの一例
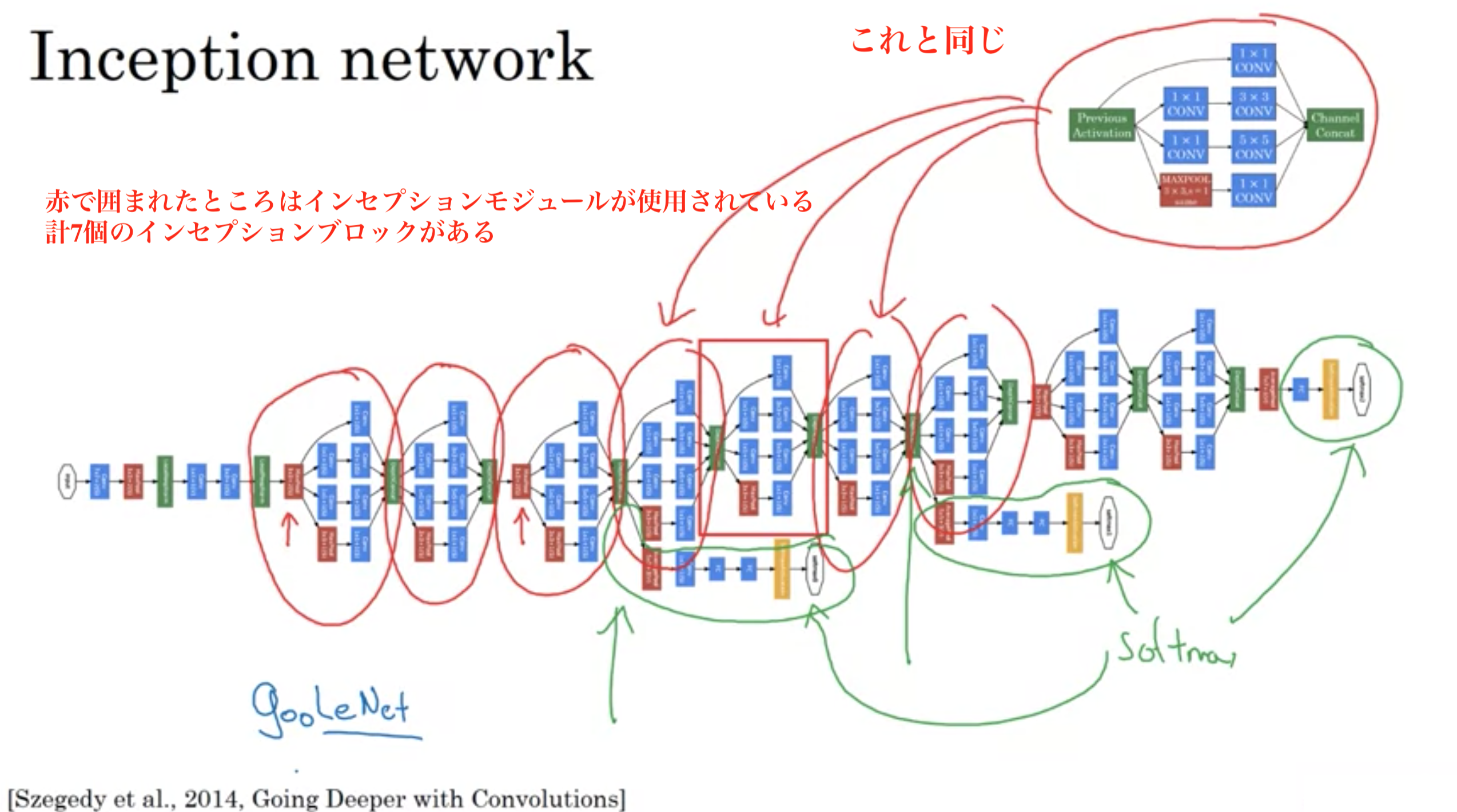 GoogLenet
GoogLenet
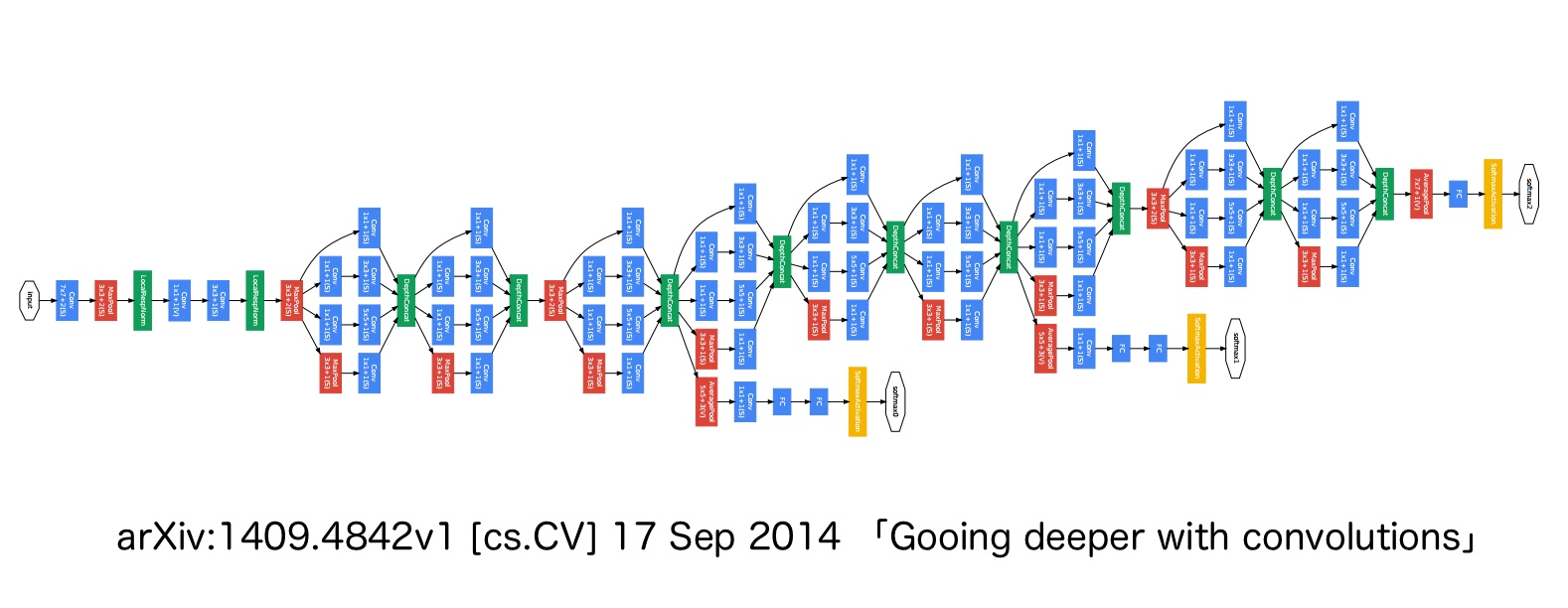 解像度
解像度
[論文] Going Deeper with Convolutions
GoogLeNet (Szegedy et al., 2014) は、VGGNet とは独立に開発されたアーキテクチャであり、2014 年の画像分類チャレンジコンテスト ISLVRC-2014 で 1 位を獲得した。GoogLeNet のアーキテクチャは、AlexNet、ZFnet などの既存のアーキテクチャとは大きく異なり、1×1 Convolution、global average pooling (Lin et al., 2014)、および Inception モジュールなどの技術が新たに導入された。GoogLeNet は、この Inception モジュールを取り入れたことで、層を深くすることができるようになり、全体で 22 層で構成されている。
これまでのアーキテクチャは、畳み込み層を順列に繋げていた。このため、畳み込み層が深くなるにつれ、画像サイズが小さくなっていき、層を深くすることができなかった。これに対して、GoogLeNet では、1 つの入力画像に対して、複数の畳み込み層(1×1, 3×3, 5×5)を並列に適用し、それぞれの畳み込み計算の結果を最後に連結している。この一連の作業をモジュールとしてまとめられ、Inception モジュールと呼ばれている。Inception モジュールを多数使うことで、パラメーターが膨大な数になる。そこで、GoogLeNet では、各畳み込み計算を行う前に 1×1 Convolution を行い、パラメーター数を削減している。
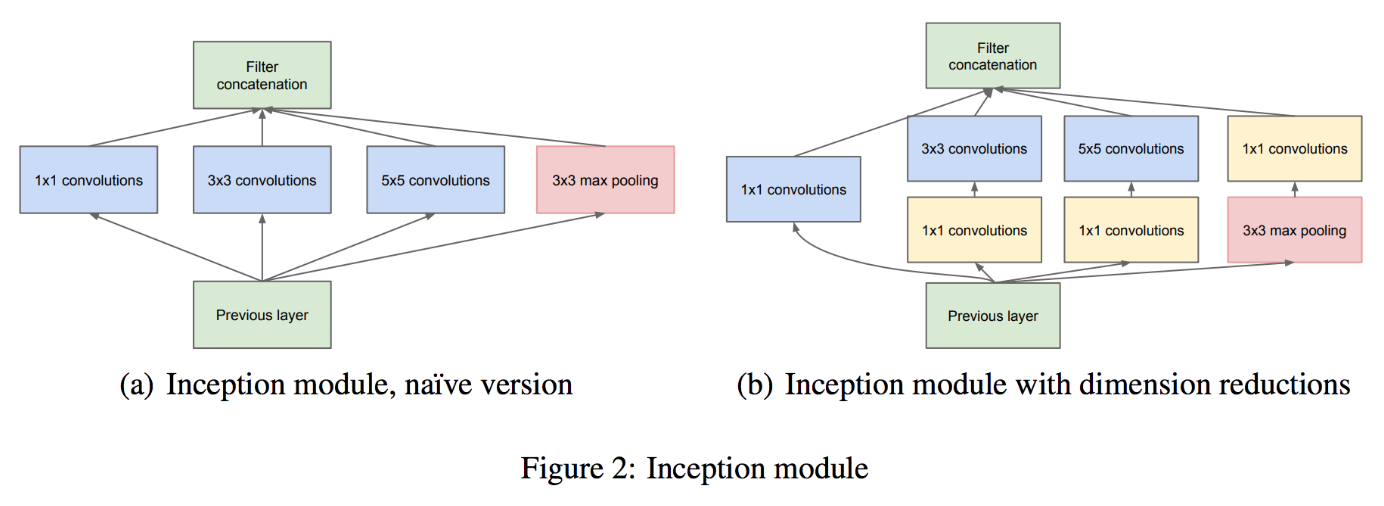
Figure 2 (a) は Inception モジュールの基本構造を示している。Figure 2 (b) は 1×1 Convolution を組み込んだ Inception モジュールの構造を示している。
従来の画像分類アーキテクチャでは、最後の層に全結合層が用いられている。全結合層では、層間のパーセプトロンが互いにすべて結合している。そのため、パラメーター数が多く、過学習を起こしやすいことが知られていた。そこで、GoogLeNet では、最後の層で全結合層の代わりに、global average pooling とよばれる技術を取り入れている。
GoogLeNet では、最後の畳み込み層において、チャンネル数をクラス数と同じになるように畳み込み計算を行っている。例えば、100 クラスの分類問題では、最後の畳み込み層で、100 チャンネルのとなるようにする。続いて、各チャンネルに対して、画素平均を計算し、最終的にはチャンネル数分の要素を持ったベクトルが得られる。このベクトルに対してソフトマックス関数を適用することで、クラスの分類結果が得られるようになる。
GoogLeNet にはいくつかのバリエーションが存在する。ISLVRC-2014 で優勝した最初に発表されたバリエーションは Inception v1 と呼ばれている。その後、Inception モジュールに含まれている畳み込みフィルターのサイズを変更した Inception v2、そして Inception v2 に対してさらに改良を加えた Inception v3 が開発された(Szegedy et al., 2015)。さらに、その後も改良が行われ、Inception v4 や ResNet を取り込んだ Inception-ResNet が開発された(Szegedy et al., 2016)。
他の人が公開したものを、論文を読むだけで真似るのが難しいことがある。
幸運なことに、ディープラーニング研究者たちは日常的に自分たちの仕事をGithubなどでインターネットにアップしている
自分のコードも同じように、オープンソースコミュニティに貢献し返すことをお勧めする。
研究論文を見て、結果の上に自分で何かを作りたいときにやった方が良いこと
・オープンソースの実装をオンラインで探す
理由: 作者の実装を入手できれば、ゼロから実装するより非常に早く開発を進められる。
(しかし、ゼロから作る場合は良い練習にもなる)
オープンソースを使うことの利点の1つは、必要なネットワークは時折長時間の学習が必要で複数のGPUととても大きなデータセットを使っていくつかのネットワークは訓練されているかもしれないということ。これにより、転移学習(transfer learning)が行える。
オープンソースコードを利用することで、新しいプロジェクトを始めるのがより良くなり、速くなる。
時折、ニューラルネットワークの訓練は数週間かかったり、とても多くのGPUを使用したりする。
例えば、猫画像の分類器(Tiger, Misty, Others)を作成したいがデータが少ない場合どうしたら良いか?
いくつかのオープンソースで実装されたニューラルネットワークをダウンロードすることを推奨。コードだけではなく、重みもダウンロードする。
ImageNetデータセットには1000個の異なるクラスがあって、ネットワークはソフトマックスで1000の内の1つを出力するだろう。
できるのは最後の出力層を取り除き、Tiger, Misty, Othersを出力する自分のソフトマックスユニットを作る。
ネットワークの方は、出力層以外は固定されたものと考えると良い。つまり、隠れ層のパラメータを固定し、ソフトマックスに関係する出力層のパラメータのみを訓練する。
他の誰かの無料の学習済み重みを使うことで、小さなデータセットでも良い性能を実現できる。
ほとんどのフレームワークでは異なるやり方で、特定の層の重みの訓練可否を指定できる。
計算を助ける1ステップは、訓練セットの全てのサンプルを使い、固定した層の活性を事前計算してディスクに一旦保存し、それらを使ってソフトマックス識別器だけ訓練を行う。
ディスクに保存する理由: 毎回訓練セットの活性を再計算する手間を省ける。(エポックのたびに訓練セットを通さなくて良い)
データセットが多少はある場合は?
TigerとMistyの画像をたくさん持っているかもしれない。そのような場合、以下の2つの方法があり、どちらもやってみる価値がある。
より少ない層を固定する (出力層だけでなく、隠れ層の終わりの方の何層かも訓練する)
もしくは
隠れ層の終わりの方の何層かを消してしまい、自分自身の新しい隠れ層を作成する
データセットがたくさんある場合?
オープンソースのネットワークと重みを全て初期化だけに使い、ネットワーク全体を訓練する。
ただし、何度も言うが、1000のソフトマックスだった場合は、3のソフトマックスが必要だから、出力ラベルを自分の扱うものに変更し、自分のソフトマックス出力が必要。
赤字のものは非常によく使われる
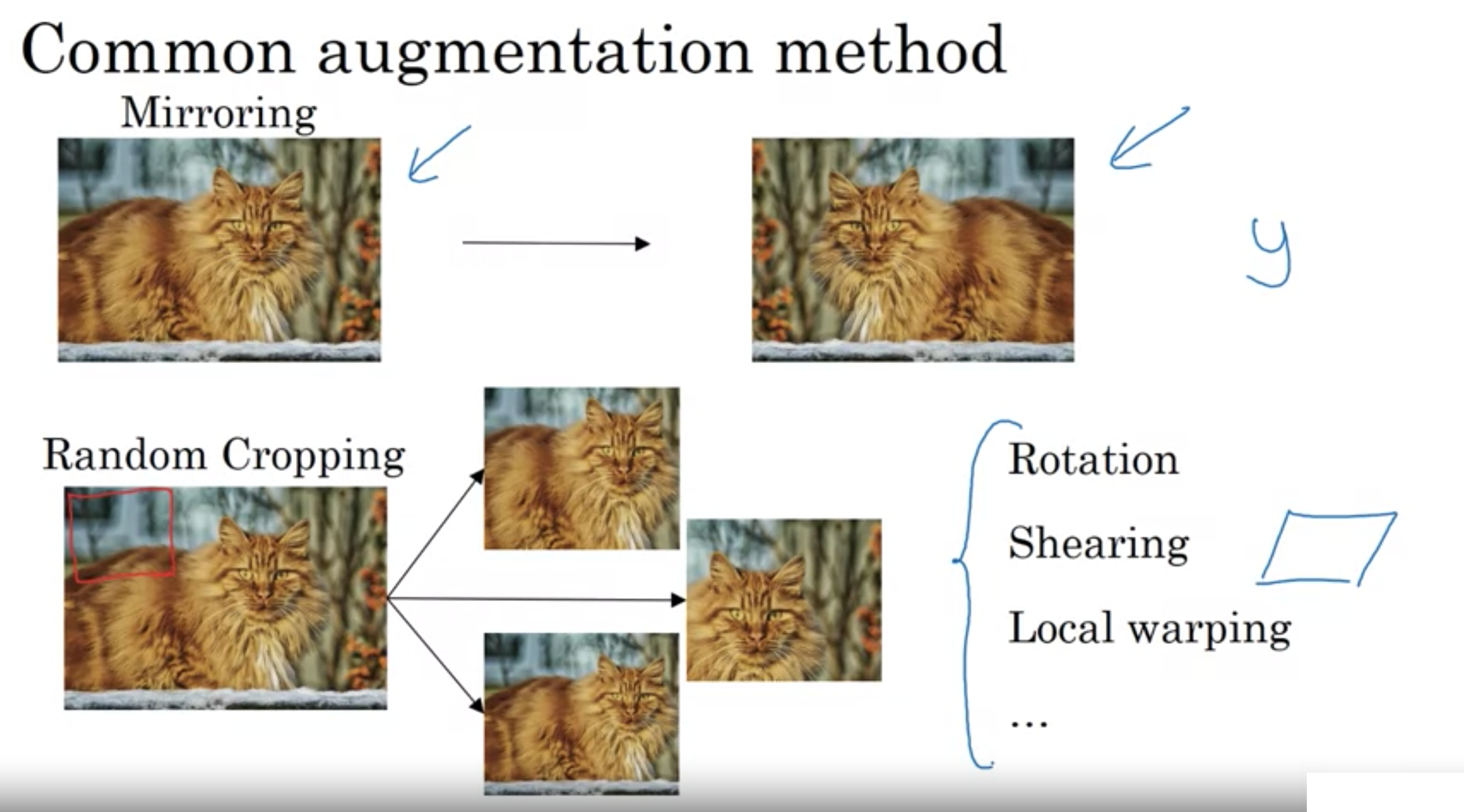
・Mirroring
ミラーリング、画像の左右を反転させる
・Random Cropping
ランダムクロップ(ランダムな切り抜き)、サイズを指定して、画像からランダムな位置を切り抜く
・Rotation
画像を任意の角度回転させる
・Shearing
画像を剪断変形、歪ませる
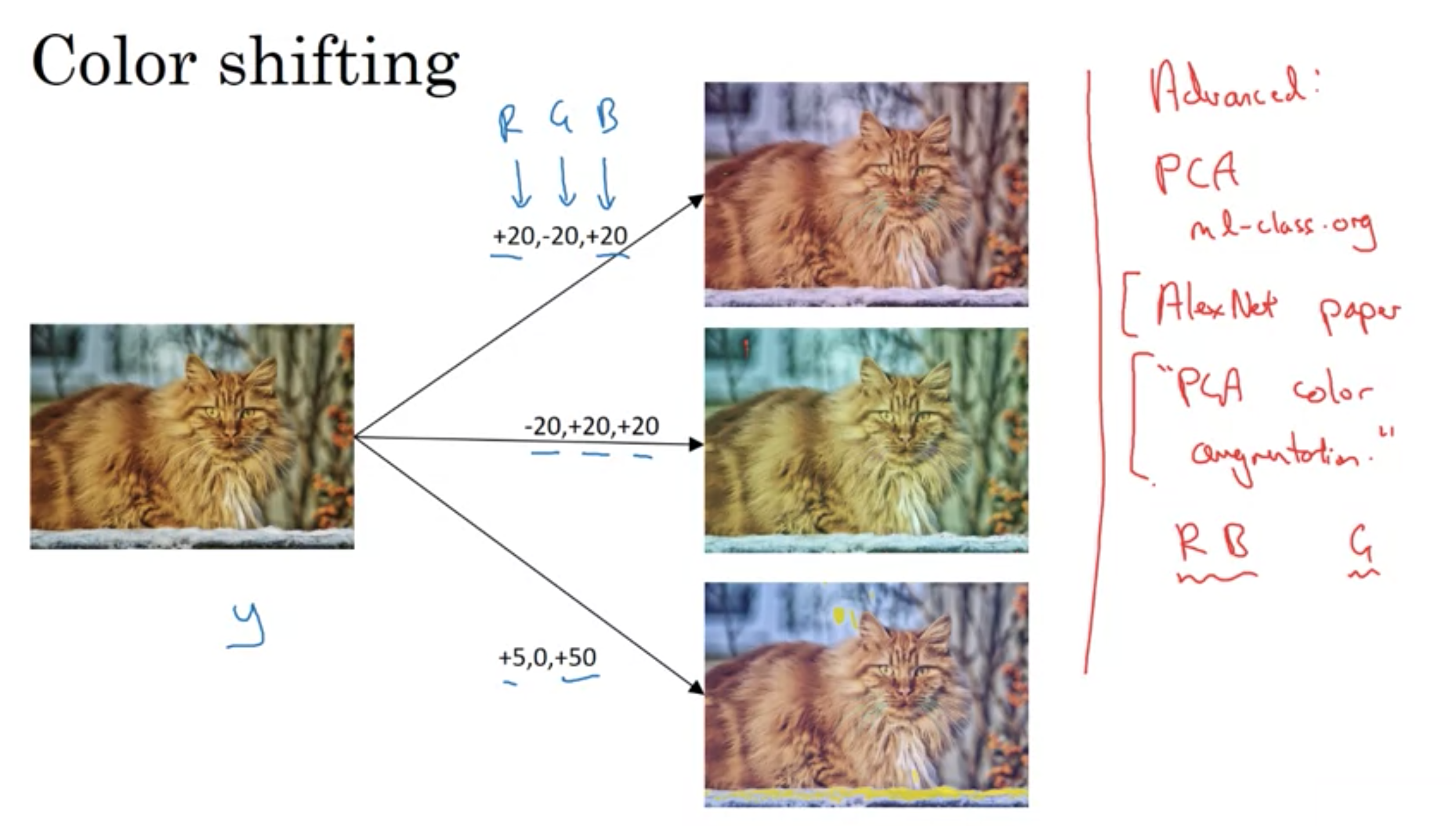
・Color Shifting
画像を変色させる、異なるRGBを使ってカラーチャンネルを乱す
ランダムクロップは完璧なデータ拡張ではない。
ランダムな切り抜きをした結果、猫の画像が猫に見えなくなったらどうする?
しかし、実際はランダムクロップが実際の画像の十分大きなサブセットである限りはやる価値がある
カラーシフティングにて色の乱れを実装する方法の1つは、PCAと呼ばれるアルゴリズムを使用すること。
"PCA Color Augmentation"と呼ばれる。
例えば、画像がもし紫だったら、主に赤と青の色合いと少しの緑を持つ 。PCA Color Augmentationは、赤と青に対して大きく足したり引いたりして、緑には少しだけ行う。そうして全体の色合いを同じに保つ。
詳細は、AlexNet論文で理解できる。
AlexNet論文 ImageNet Classification with Deep Convolutional Neural Networks
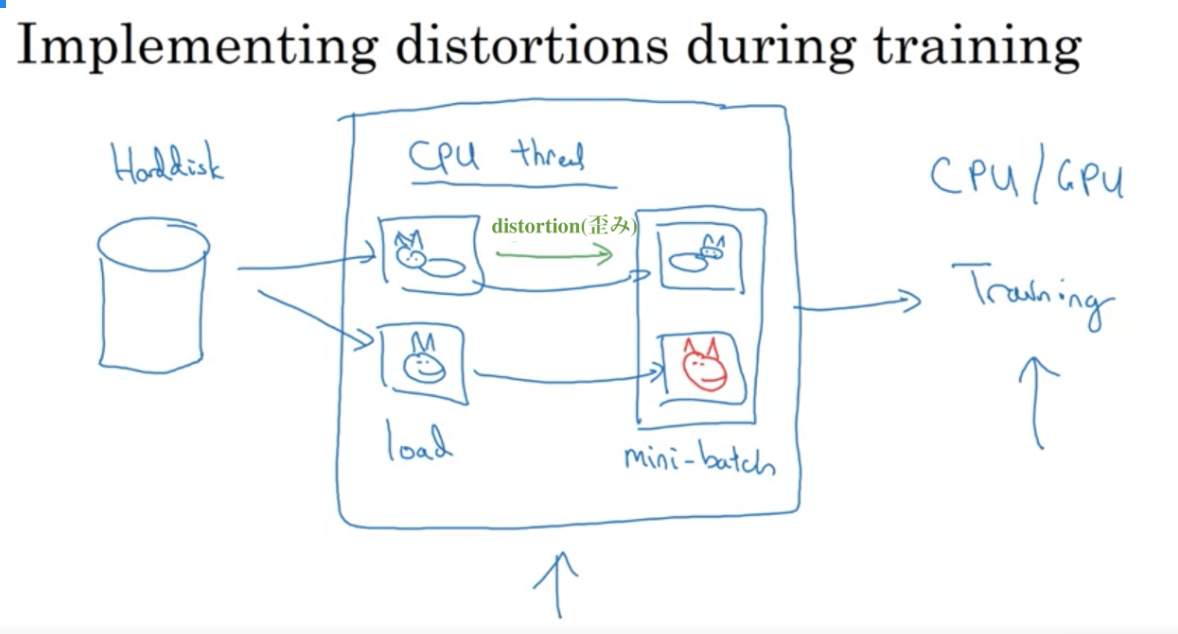
データセットが大きい時の手法
1つのCPUスレッドを使ってハードディスクから連続して画像を読み込み、1つのCPUスレッドを使ってねじれを作る。ランダムプロップや変色、ミラーリングを行う。
 データ拡張の手法
データ拡張の手法
 カラーシフトによるデータ拡張
カラーシフトによるデータ拡張
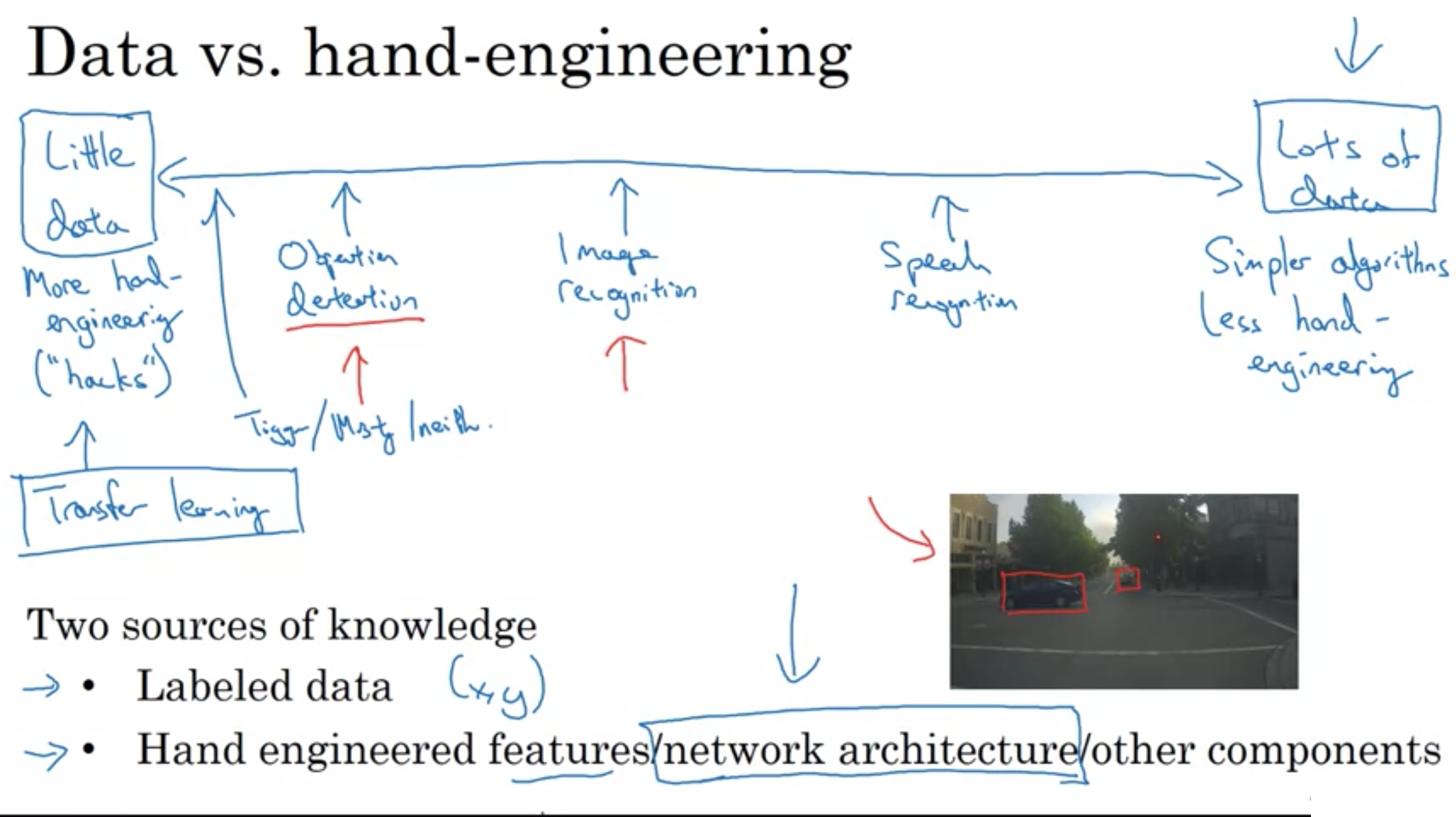
今日、音声認識のデータセットは豊富で、画像認識のデータはまあまあ存在し、物体検出においてはあまりデータがない。
データがあまりない場合、データを増やす自動的な手法を求めたくなるが、手作業での調整が実際良い性能を得るための一番の方法である。
機械学習では2種類の知識がある
・Labeled data
ラベル付されたデータ (教師あり学習で使う、xとyのペア)
・Hand engineered features/network architecture/other components
手作業で調整したデータ(特徴量を注意深く設計することからネットワークを注意深く設計することまで色々ある)
手作業での調整に多く頼る理由
コンピュータビジョンでは、必要なデータが足りないということがよくあるから
ニューラルネットワークが、より複雑なネットワーク構造を発展させてきた理由
データが足りない中で良い性能を得るためのネットワーク構造を計算し、工夫を凝らしてきた
・Ensembling
(個別でいくつかのネットワークを訓練し、出力を平均する)
出力を平均する上で重要なのは、上手く働かない重みは平均しないこと
弱点: いくつかネットワークを保持して時刻するため、多くのメモリが使われる
・Multi-crop at test time
テスト画像にもデータ拡張を使用する
テスト画像の複数のバージョンで識別器を実行し、結果を平均する 例えば 10-crops がある
弱点: 実行時間がかなり長い
例えば3~15のネットワークでアンサンブルした場合、テスト時も複数のネットワークに画像を通さなければならないので、実行時間が3~15倍かかってしまう。そのため、顧客に提供する場合は決して使わない。(あくまで、ベンチマークを上手くやり、コンペティションで勝つためのコツ)
 データと手動調整
データと手動調整
 コンペで勝利したりベンチマークで上手く機能させるコツ
コンペで勝利したりベンチマークで上手く機能させるコツ

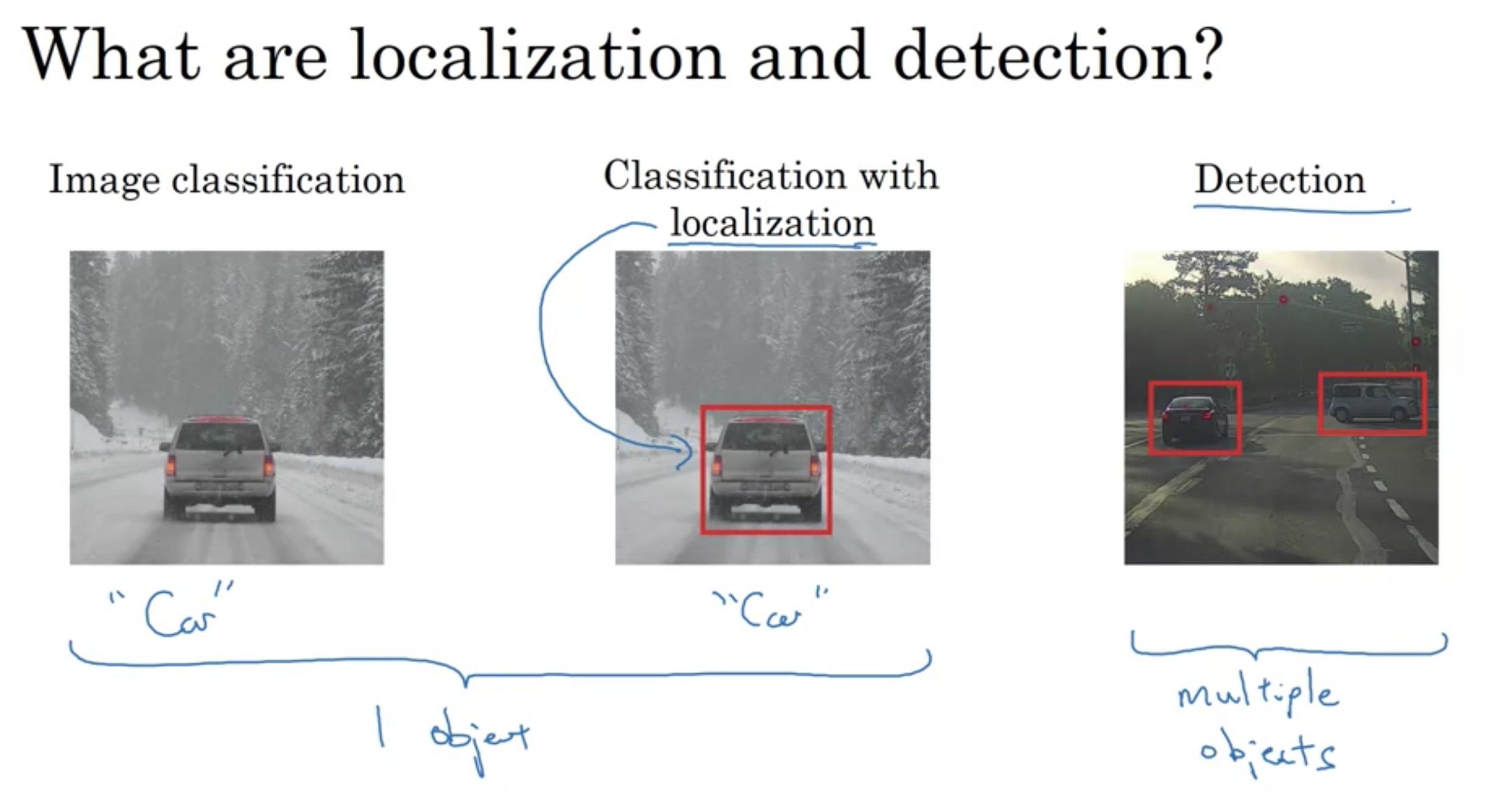 位置の特定と検出
位置の特定と検出
画像分類: 1つのオブジェクトを分類
位置での分類: 1つのオブジェクトを分類
物体検出: 複数のオブジェクト
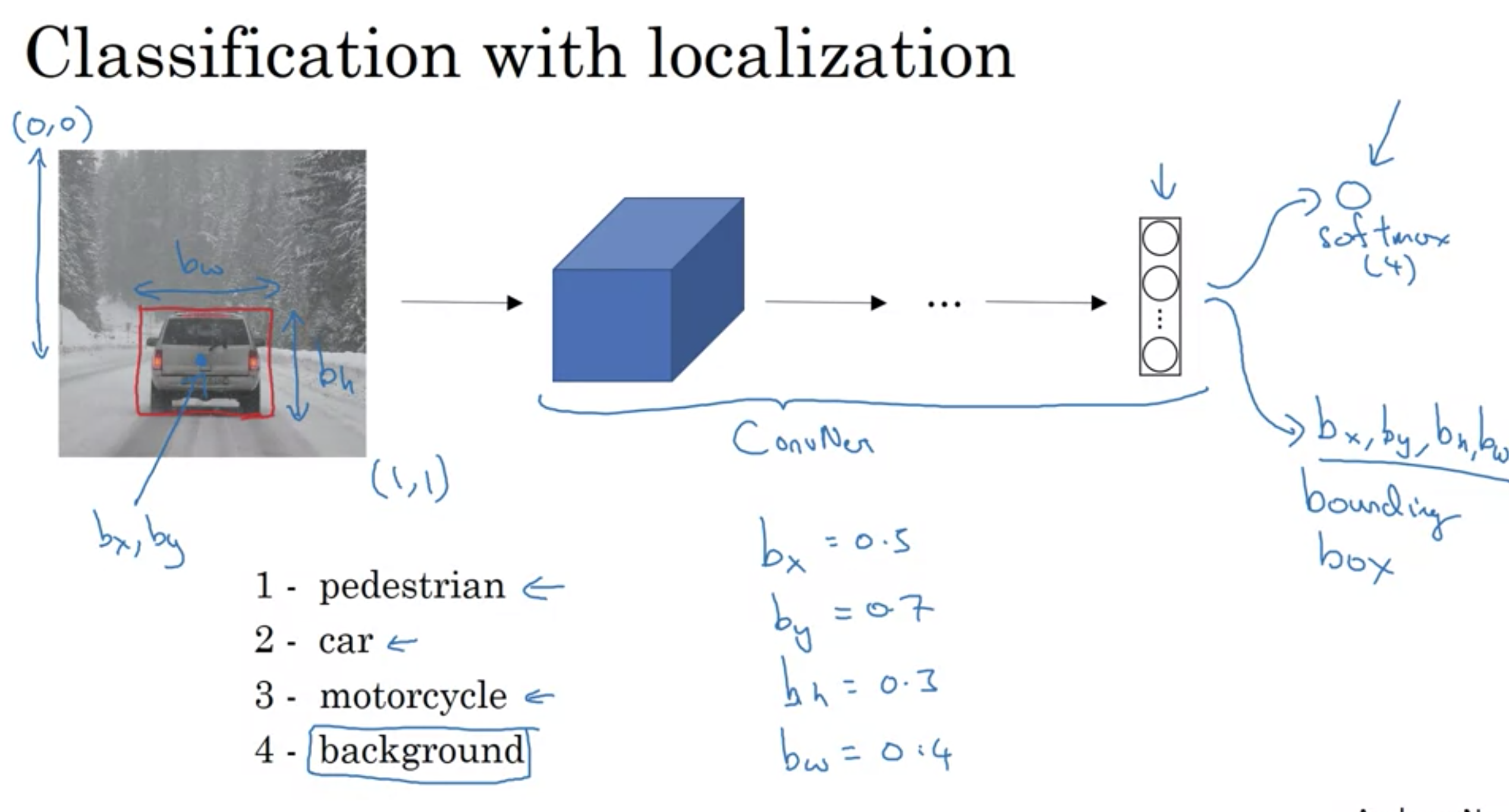 位置での分類
位置での分類
オブジェクトのバウンディングボックスは、以下の数値から作成される
・オブジェクトの中心座標 (\( b _{ x } \), \( b _{ y } \))
・オブジェクトの高さ \( b _{ h } \)
・オブジェクトの幅 \( b _{ w } \)
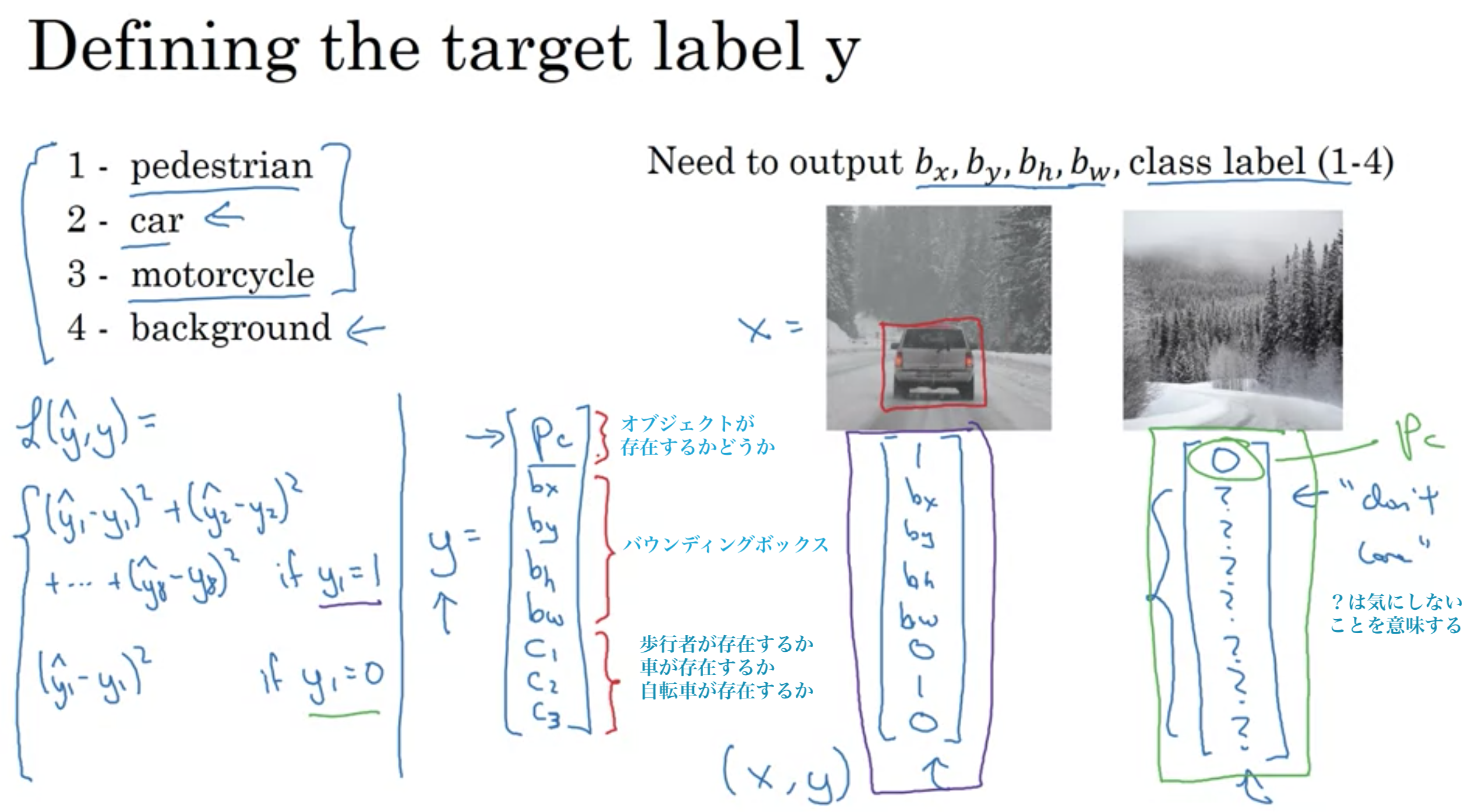 ターゲットラベルyの定義
ターゲットラベルyの定義
位置決め付き分類問題はマルチタスク学習
\( p _{ c } \): オブジェクトが存在するか
\( c _{ 1 } \): 歩行者が存在するか
\( c _{ 2 } \): 車が存在するか
\( c _{ 3 } \): 自転車が存在するか
バウンディングボックスでは4つの数字 \( b _{ x } \), \( b _{ y } \), \( b _{ h } \), \( b _{ w } \)を出力するニューラルネットワークを作る。
このような、ニューラルネットワークが出力する画像中の重要な座標をランドマークと言う。
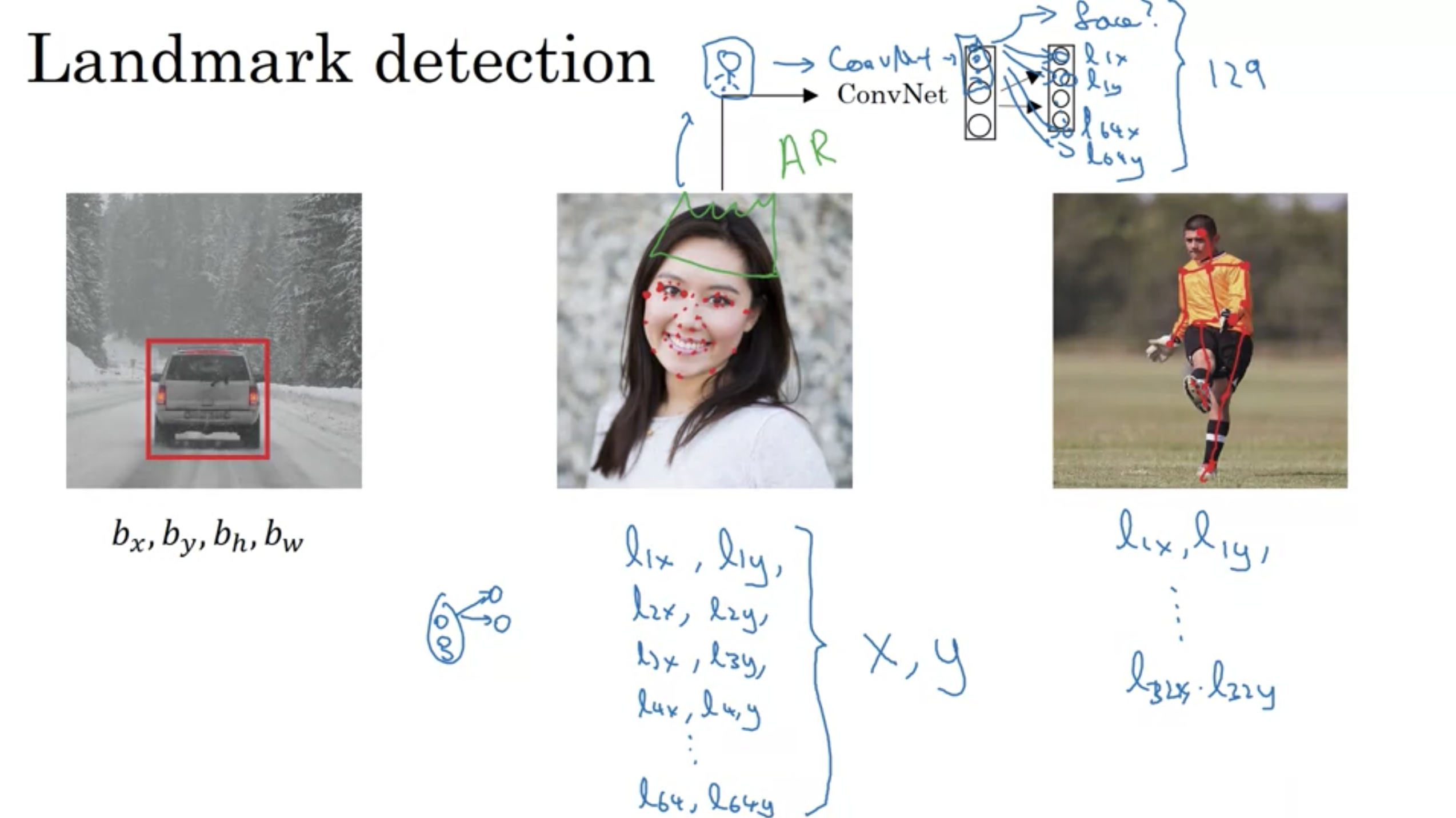 ランドマーク検出
ランドマーク検出
画像の表情が笑っているかを判断するために、顔の目や口周りに64個のランドマークがあるとする
顔のランドマークを検出するニューラルネットワーク ConvNetの出力ユニット 129個
・顔があるかどうか
・ランドマーク1のx, y
・ランドマーク2のx, y
...
・ランドマーク64のx, y
SnapsnatやSnowなどで、顔を歪ませたり王冠や帽子を載せたりする拡張現実のフィルターも顔のランドマークの検出を利用している。
最後に、人のポーズ検出
例えば、ボールを蹴っているポーズは、胸の真ん中、左肩、左肘、手首などをランドマークとして、ニューラルネットワークに人のポーズの主な位置を出力させる。
 車の検出
車の検出
スライディングウィンドウ検出アルゴリズム
ConvNetに四角の小さいウィンドウを入力する。
画像内の全ての位置にウィンドウをスライドさせるまで続ける。
 スライディングウィンドウ検出
スライディングウィンドウ検出
しかし、スライディングウィンドウには大きな欠点がある
とても多くの異なる四角の領域を切り抜いてそれぞれを個別にConvNetにかけるから。
非常に荒い(大きな)ストライドを使えばConvNetを通すウィンドウの数は減るが、性能は落ちる。
とても細かい粒度のストライドを使えば、計算コストが高くなる。
昔は単純な線形関数の分類きだったので、計算コストがかからなかったが、ConvNetでこのやり方はとても高価で実行不可能なほど遅い。
そこで解決策が次に続く。
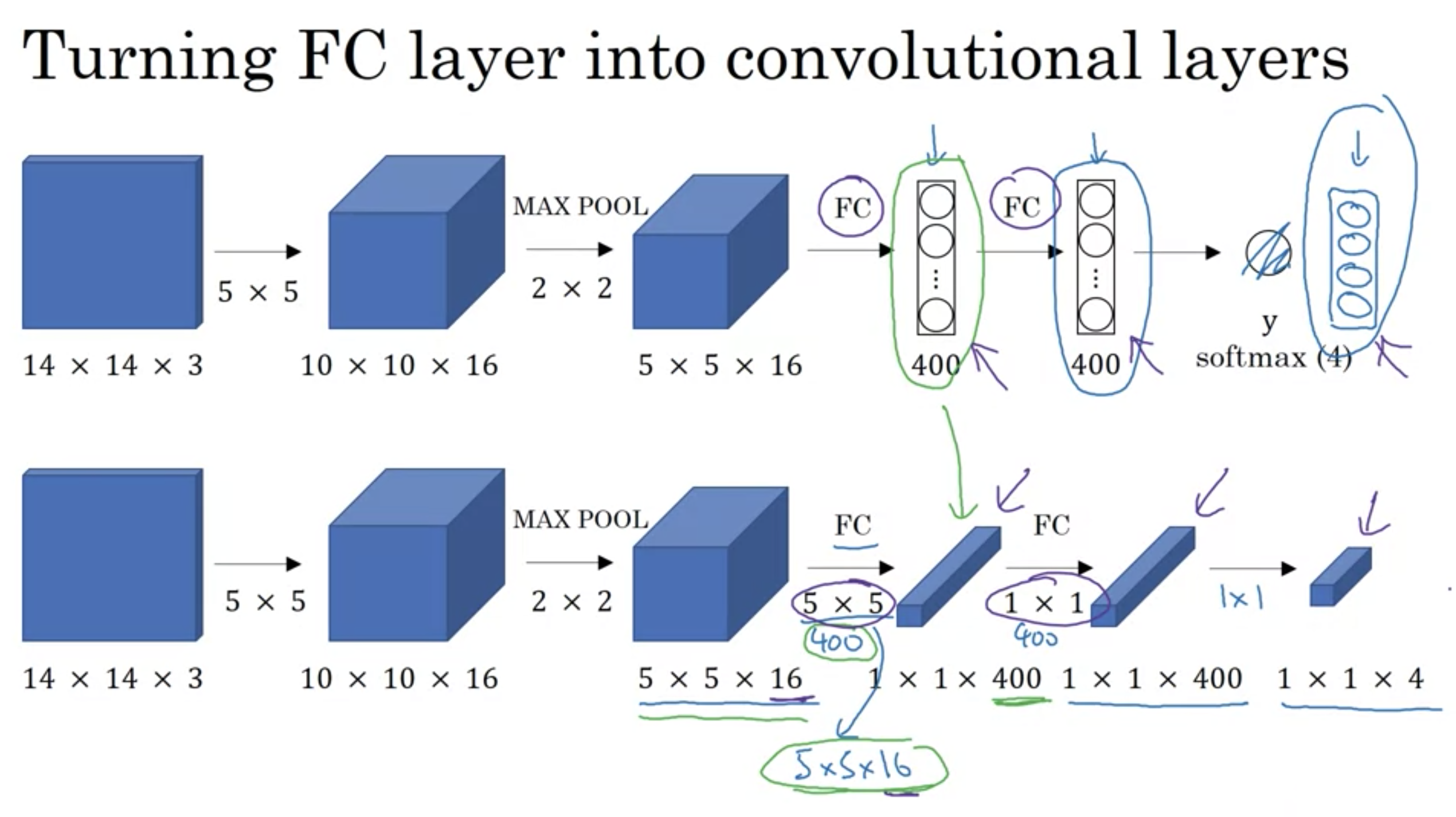 全結合層を畳み込み層へ変換
全結合層を畳み込み層へ変換
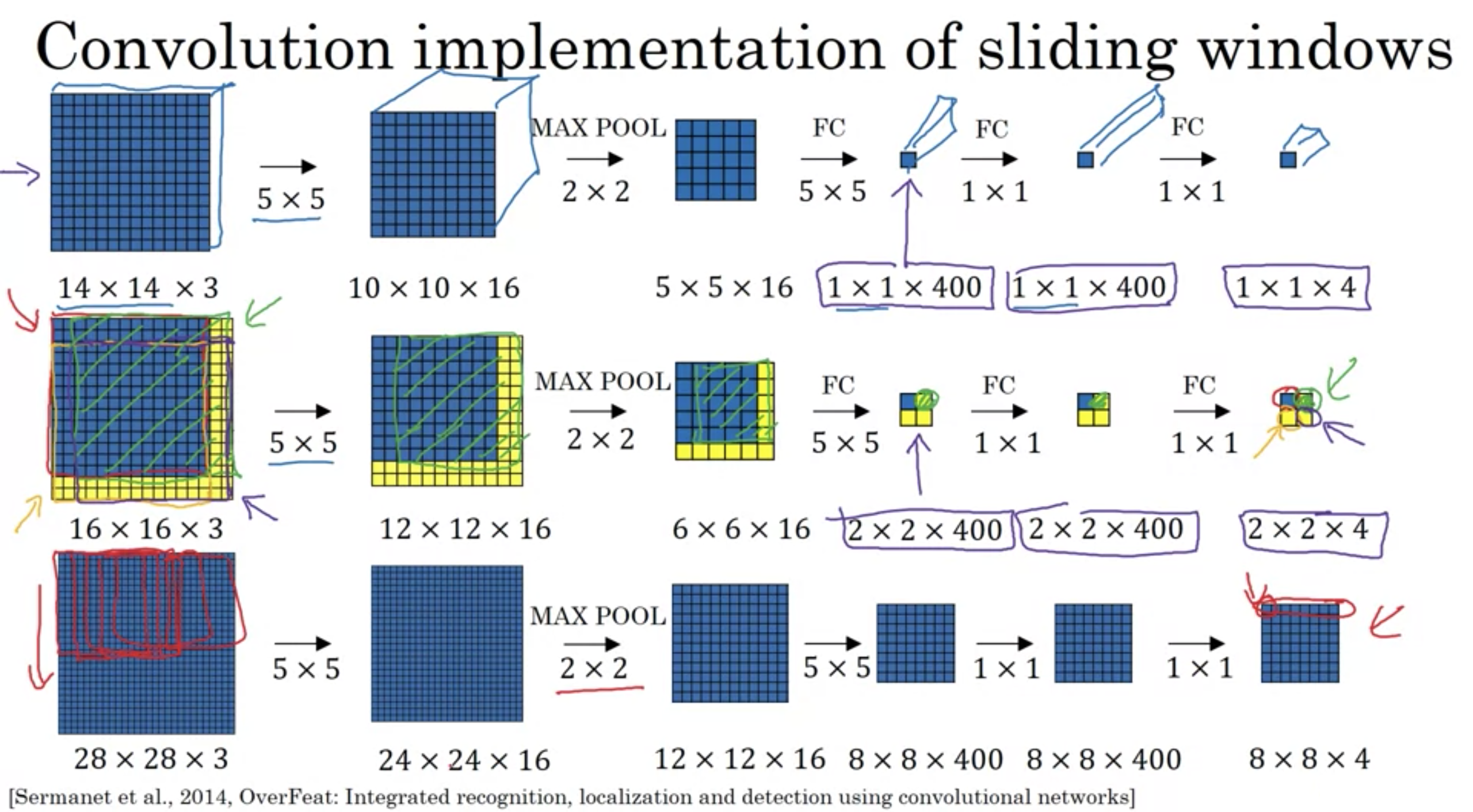 スライディングウィンドウの畳み込み
スライディングウィンドウの畳み込み
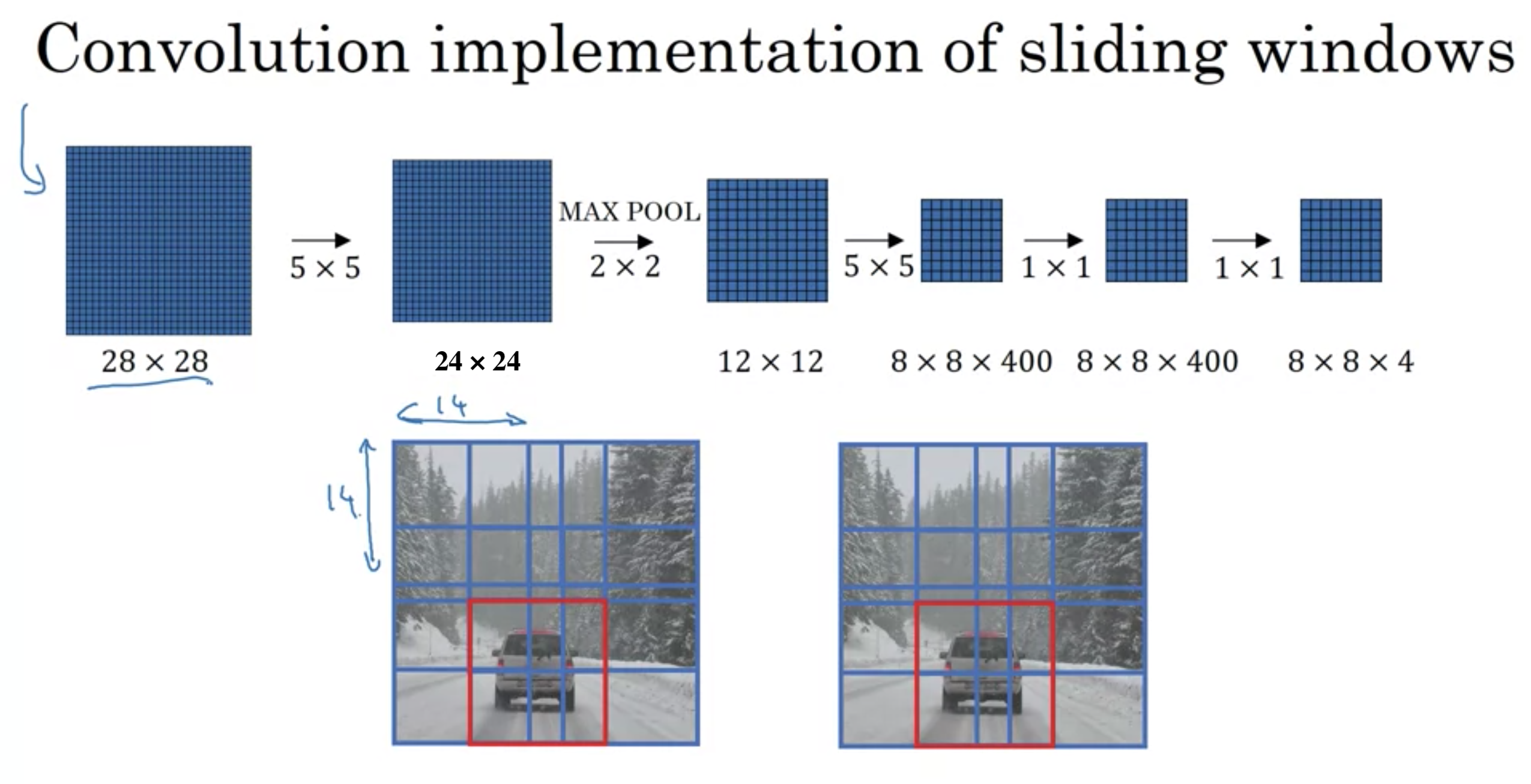 スライディングウィンドウの畳み込み実装
スライディングウィンドウの畳み込み実装
この手法で計算コスト問題は解決される。
しかし、このスライディングウィンドウの畳み込み実装の欠点バウンディングボックスの位置がそれほど正確にならない。
この問題の修正方法が次に続く。
スライディングウィンドウでは、ウィンドウの位置や大きさが正確にバウンディングボックスと一致させるのが難しい。
正確なバウンディングボックスを出力させる方法
YOLOアルゴリズム(You Only Look Onceの略)
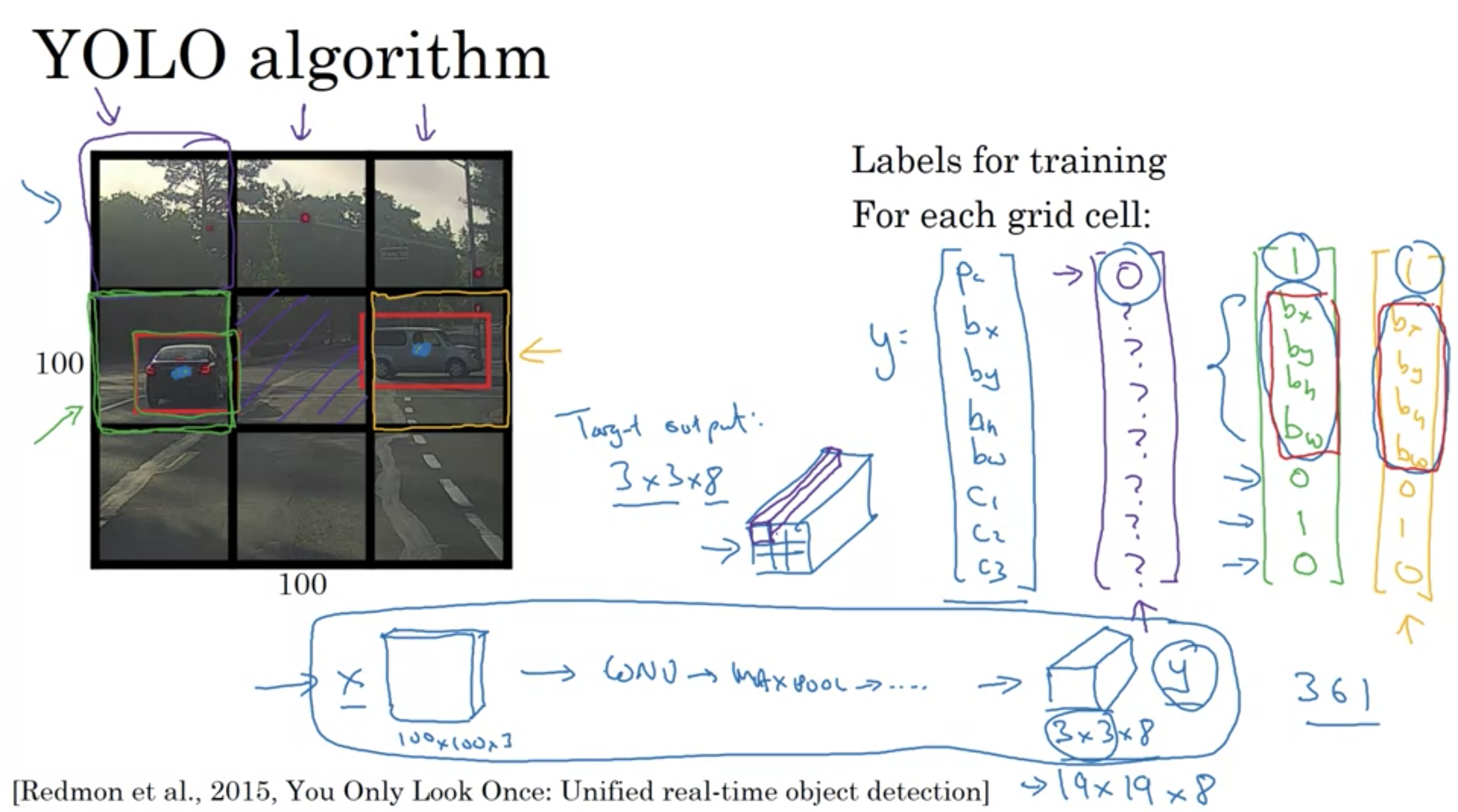 YOLOアルゴリズム
YOLOアルゴリズム
参考文献 [Redmon et., 2015, You Only Look Once: Unified real-time object detection]
画像をいくつかの格子に分割(例えば高さ19×幅19)
オブジェクトの中心座標が格子に含まれていたら、ラベルをtrueにする(オブジェクトの端が入っていても中心座標が含まれていない場合はfalse)
格子が2つ以上のオブジェクトを含まない限り、このアルゴリズムは上手くいく
 物体検出の評価
物体検出の評価
IoU: 物体検出の評価指標
ウィンドウとバウンディングボックスの重なった大きさ
$$\frac{ (ウィンドウ\cap正解バウンディングボックス) }{ (ウィンドウ\cup正解バウンディングボックス) } $$
IoCが0.5以上なら"正しい"
慣例的に0.5が使われるが、より厳密に評価したい場合は0.6や0.7を使用すれば良い。0.5以上であれば普通は良いと言われている。
IoCは0以上1以下で、完全に重なった場合、1になる
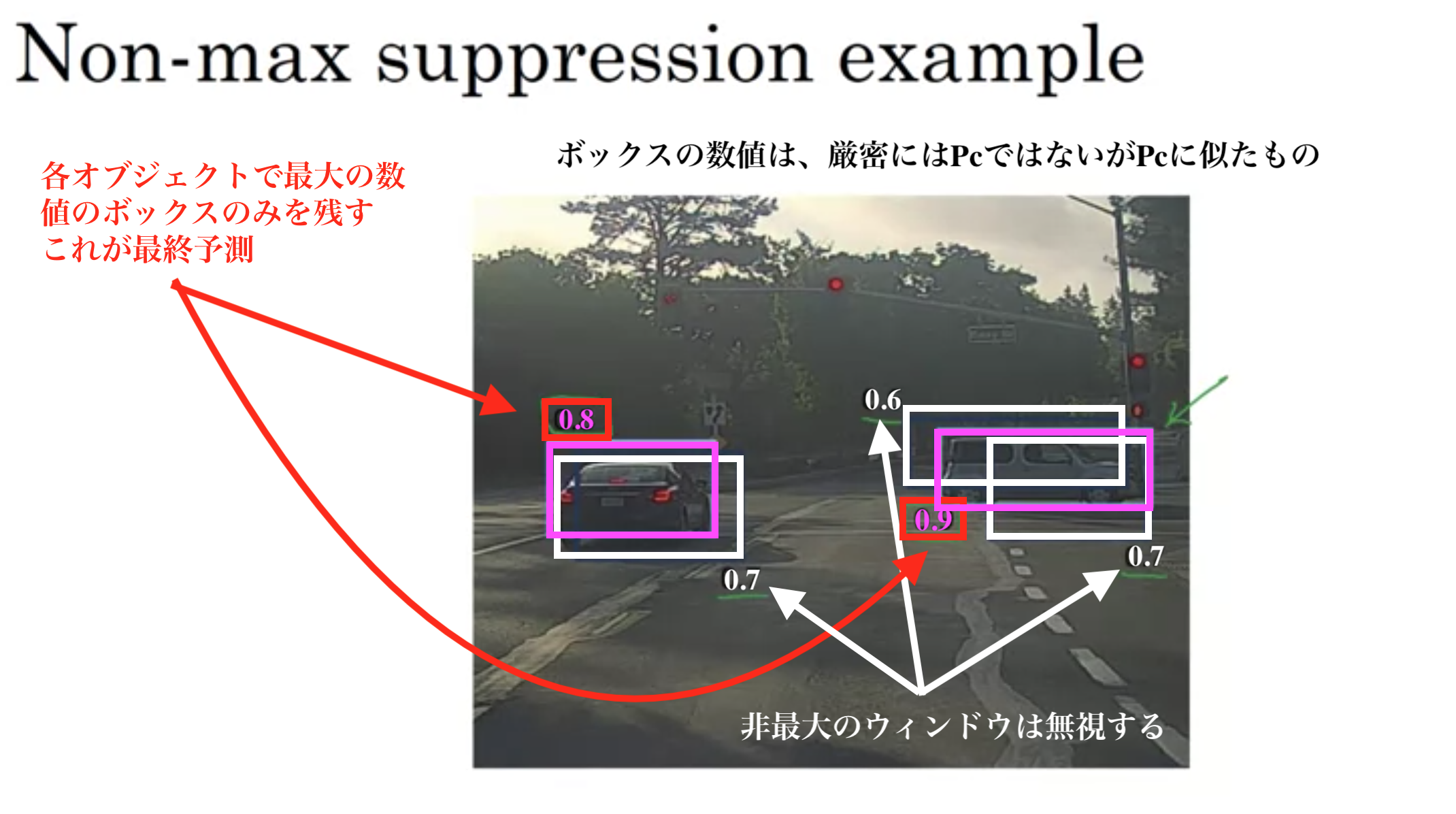 非最大抑制
非最大抑制
物体検出の問題: 同じ物体を何回も検出してしまう
Non-max Suppression(非最大抑制)はIoUが最大のもの以外を無視するすることで、1オブジェクトにつき1回しか検出しないようにする手法。
手順
1. 複数のバウンディングボックスの存在確率が閾値(例えば0.4)以下のボックスを全て削除する。
2. 1つのオブジェクトに対して、IoUが0.5以上のものが複数あった場合、IoUが最大のウィンドウをオブジェクトの境界だと決定して、それ以外のウィンドウは無視する。
 非最大抑制アルゴリズム
非最大抑制アルゴリズム
画像を19×19の格子に分割する
ConvNetで出力
\({y} = \left( \begin{array}{c} p_c \\ b_x \\ b_y \\ b_h \\ b_w \end{array} \right)\)
\(p_c \leq 0.6\)のボックスを全て破棄する
ボックスが残っている場合、以下の動作を繰り返す
・\(p_c\)(オブジェクトの存在確率)が最大のボックスを選択し、存在確率の予測値として出力する。
・前のステップのボックス出力でIOUが0.5以上の残りのボックスを破棄する
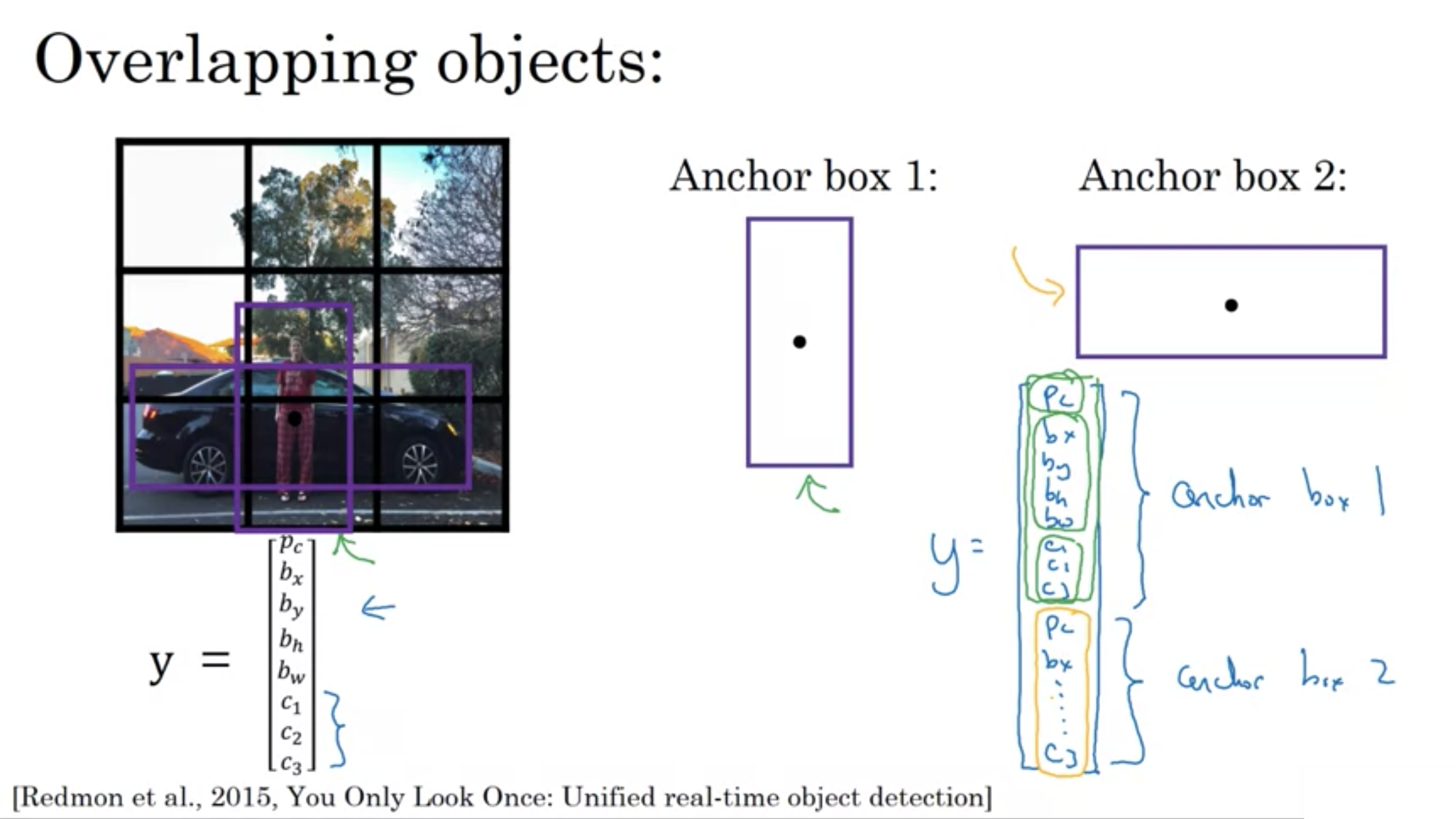 重なりあうオブジェクト
重なりあうオブジェクト
 アンカーボックスのアルゴリズム
アンカーボックスのアルゴリズム
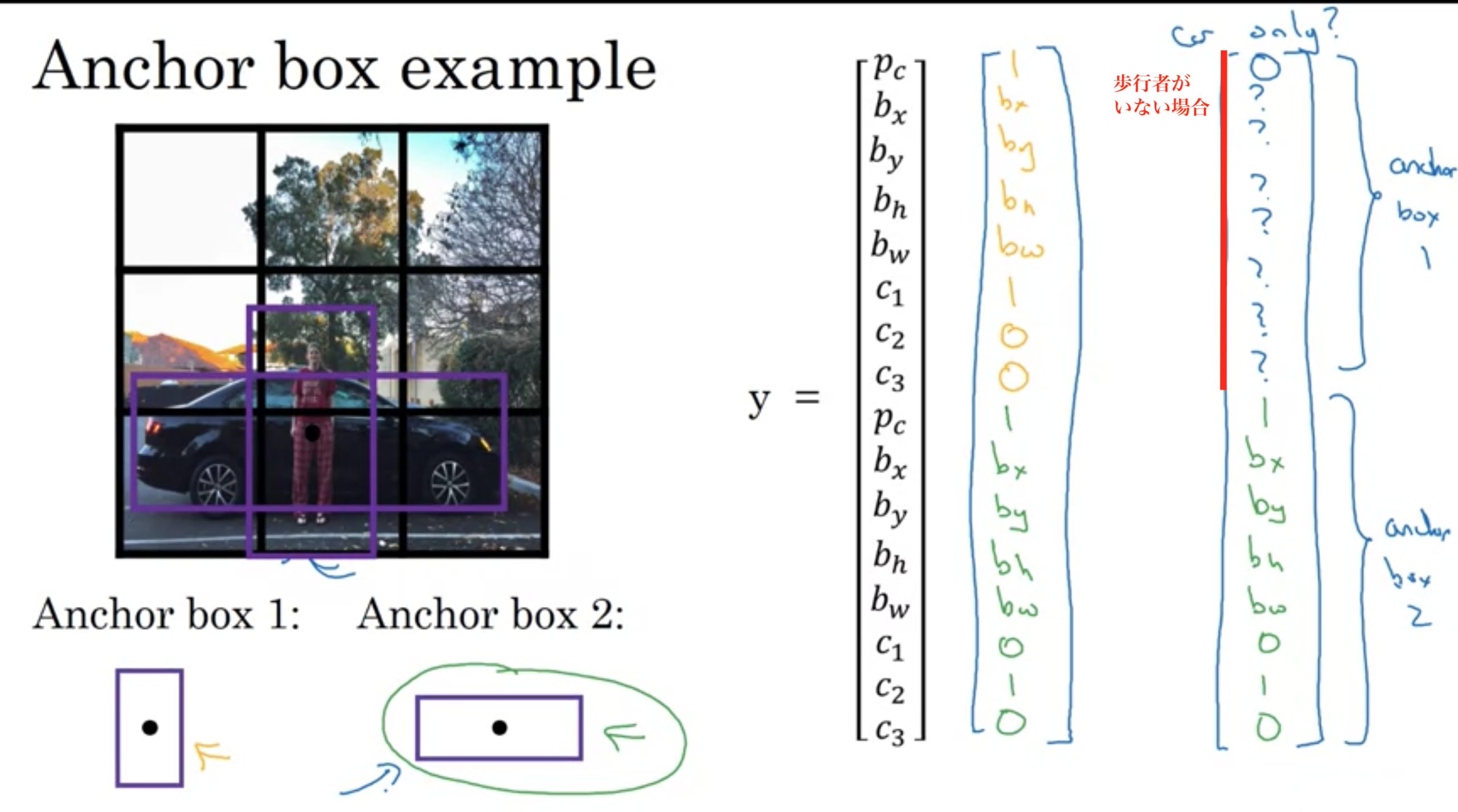 アンカーボックスの例
アンカーボックスの例
これまで学んできた物体検出の問題の1つが、それぞれの格子セルがたった1つの物体しか検出できないことだ。
アンカーボックスを使うことで、2つの物体を検出できる。
・2つのアンカーボックスがあるときに3つの物体が同じ格子に存在した場合
このアルゴリズムでは上手く処理できない。その場合はなんらかのタイムブレーク処理を実装する。
・同じ格子セルに2つの物体が紐付き、それらは同じアンカーボックスの形をしている場合
再びこのアルゴリズムでは上手く処理できない。その場合はなんらかのタイムブレーク処理を実装する。
3×3のような荒い格子fではなく、19×19の格子を使っている場合、同じセルに2つの物体が361個のセルの中の1つに同じ中心点を持つことはそんなに頻繁には起きない。
検出したい物体の種類に対応した様々な形を手動で選んだり、5~10のアンカーボックスを選ぶことが多い。
自動でのやり方: k-meansアルゴリズム 検出したい2種類の形をグループ化し、それを使ってアンカーボックスのセットを選ぶのに使う。
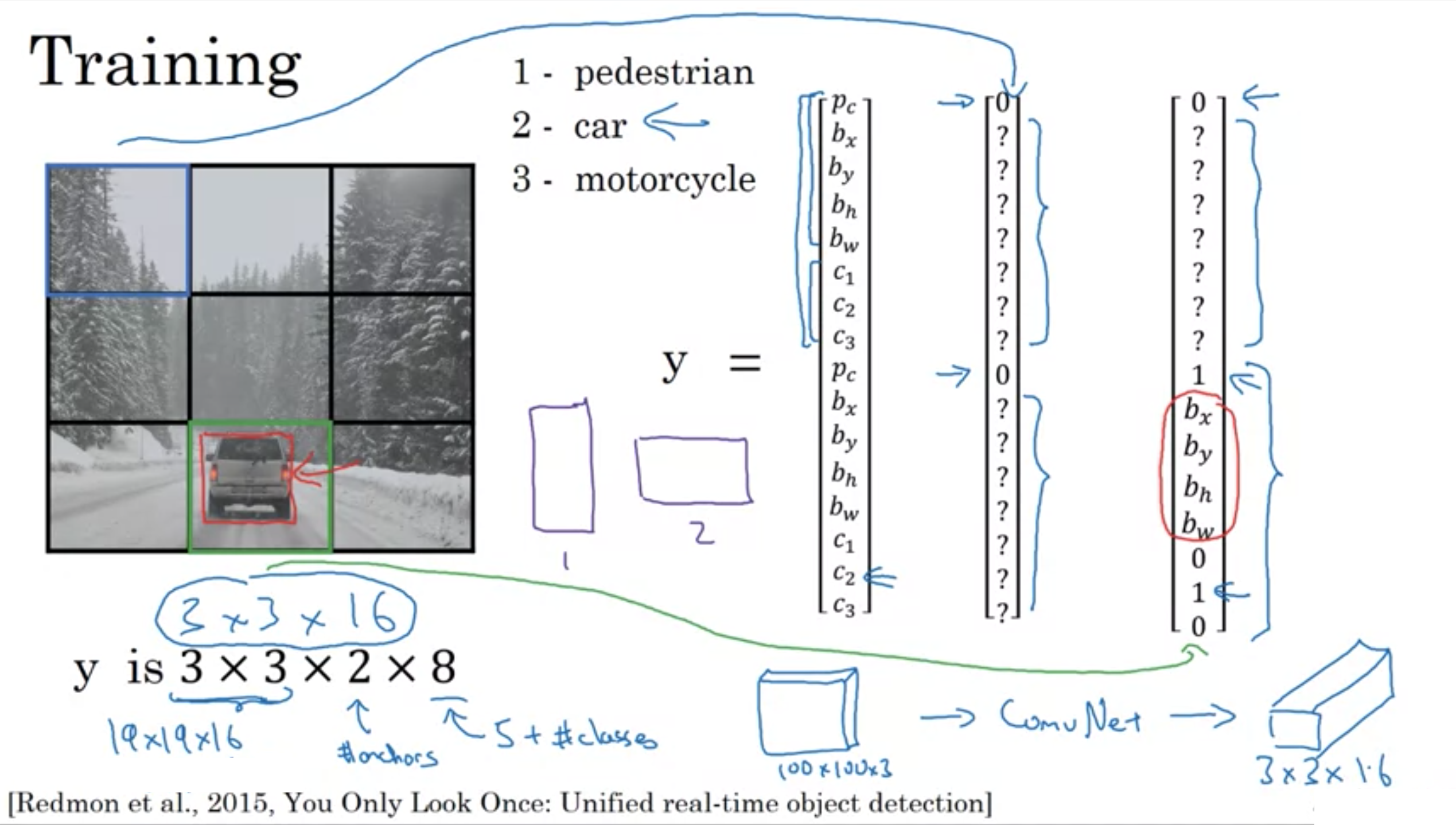 YOLOアルゴリズムの訓練
YOLOアルゴリズムの訓練
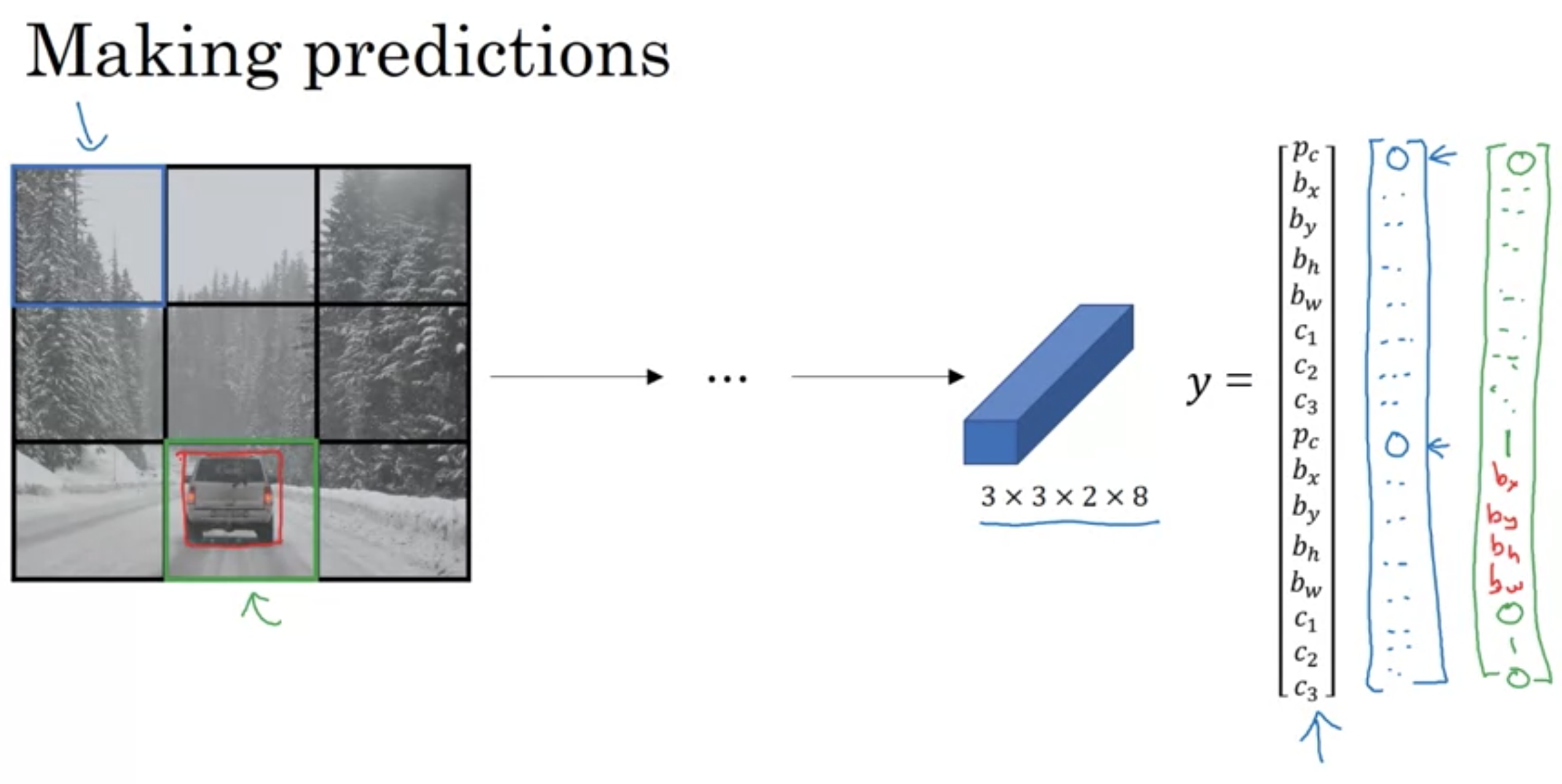 YOLOアルゴリズムの予測
YOLOアルゴリズムの予測
1. それぞれの格子で2つの予測されたボックスを取得
2. 存在確率が低いものを取り除く
3. 最終的な予測を生成するために、それぞれのクラスに非最大抑制を行う。



領域候補を使って計算するCNNのこと。
スライディングウィンドウは、画像全体の領域をスライドさせてCNNに入力する
Region Proposal (領域候補)は、少数のウィンドウを選んでCNNに入力する。
候補領域を出すには、セグメンテーションと呼ばれるアルゴリズムを利用する。
これにより、物体であり得る部分を識別する。
セグメンテーションを実行すると、200子くらいの模様を見つけるかもしれない。
その2000個にバウンdねxイングボックスを置き、2000の模様にだけCNNの計算を行う。
これで、画像全体でスライディングウィンドウを行うより、場所の数はとても少なくなるだろう。
R-CNN: 領域の候補を絞る。領域候補を1つずつ分類する。ラベルとバウンディングボックスを出力する
Fast R-CNN: 領域の候補を絞る。全ての候補領域を分類するために、スライディングウィンドウの畳み込み実装を使用する。
More Fast R-CNN: 領域の候補を作るために、(セグメンテーションの代わりに)畳み込みネットワークを使用する
しかし、速度改良(More Fast R-CNN)でも、YOLOアルゴリズムよりかなり遅いままだ。

One Shot Learning: 一般にークラスに一枚の画像しかない学習タスクをOne Shot Learningと呼ぶ
歴史的には、たった1つのデータではディープラーニングのアルゴリズムは機能しない
データベースに、それぞれの顔が1枚だけ保存されている。
例えば、CNNで多クラス分類器を使っても、データが1つしかないので、うまくはいかない
そこで、類似度関数を使う。
2枚の画像の異なり具合を数値化し、閾値を超えた場合は別人、閾値以下では同じ人と判断する
 類似度関数
類似度関数
画像の距離関数の定義にシャムネットワークを使う
距離関数d: \( {\displaystyle d(x^{(1)},x^{(2)}):=|| f(x^{(1)})-f(x^{(2)}) || _{ F } }\) Fはフロベニウスノルムを表す記号
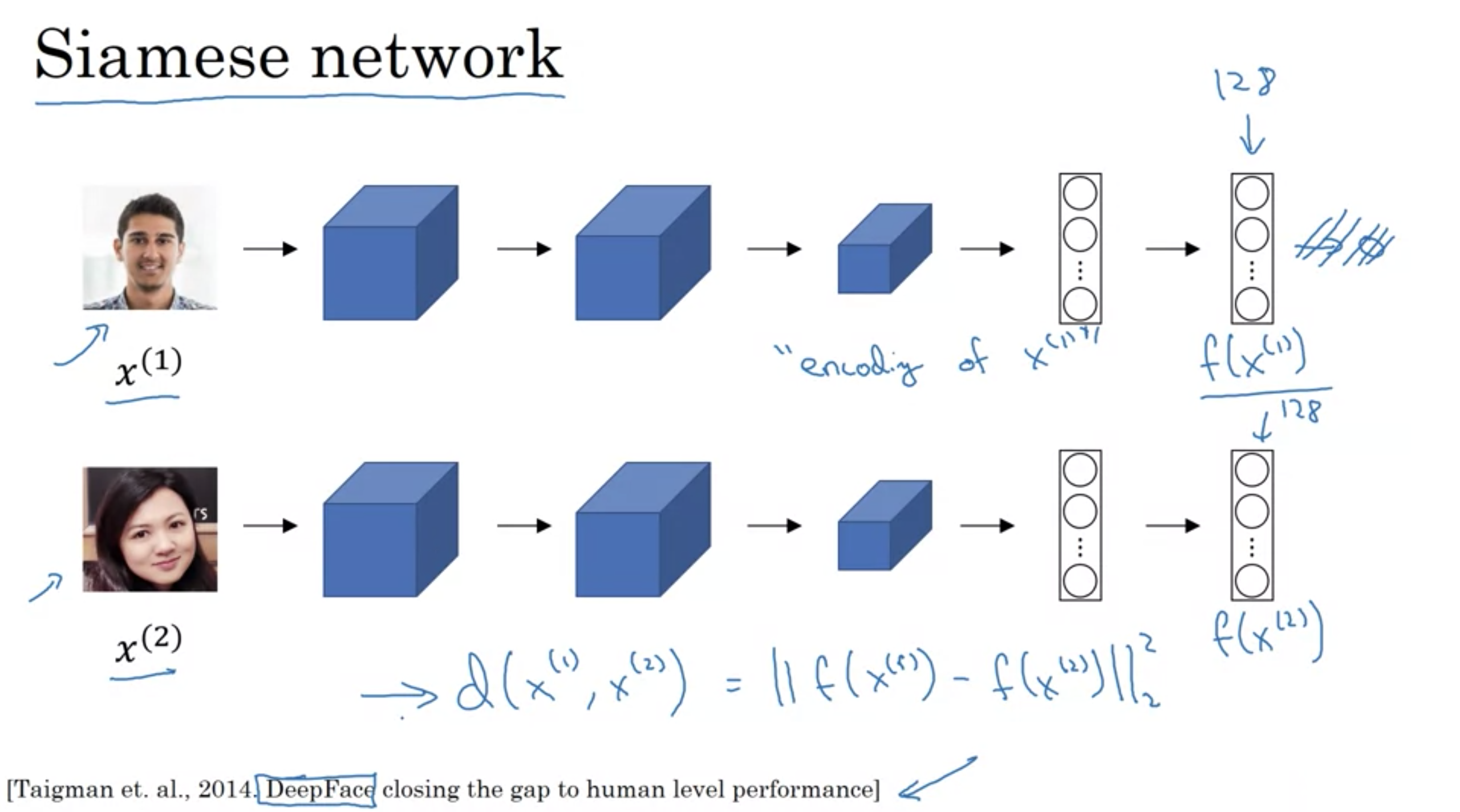 Siamese Network
Siamese Network
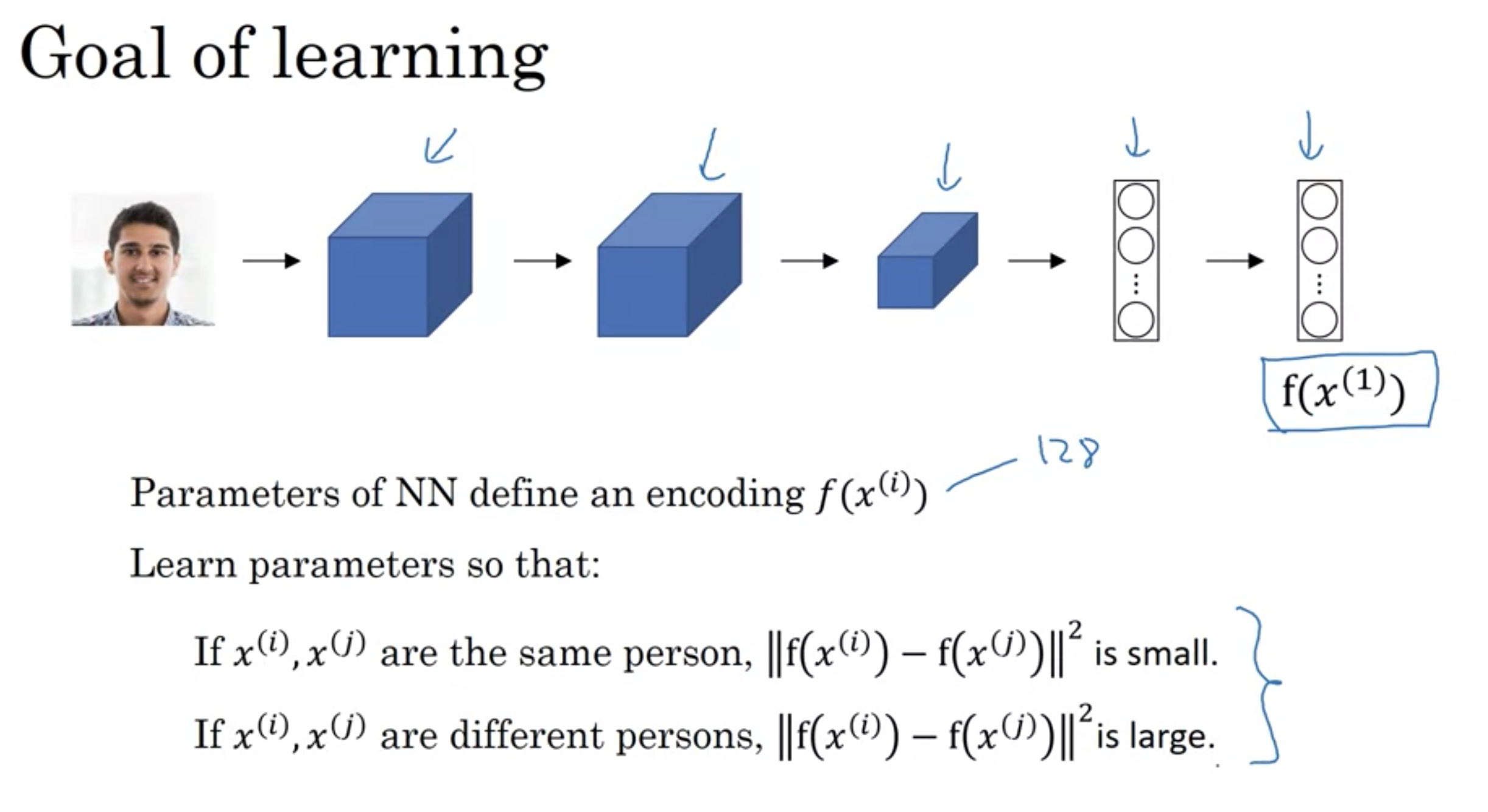 学習の目標
学習の目標
三重項損失関数

 Triplet function
Triplet function


以下の上と下のConvNetは、入力画像は違うが、パラメータは全く同じ
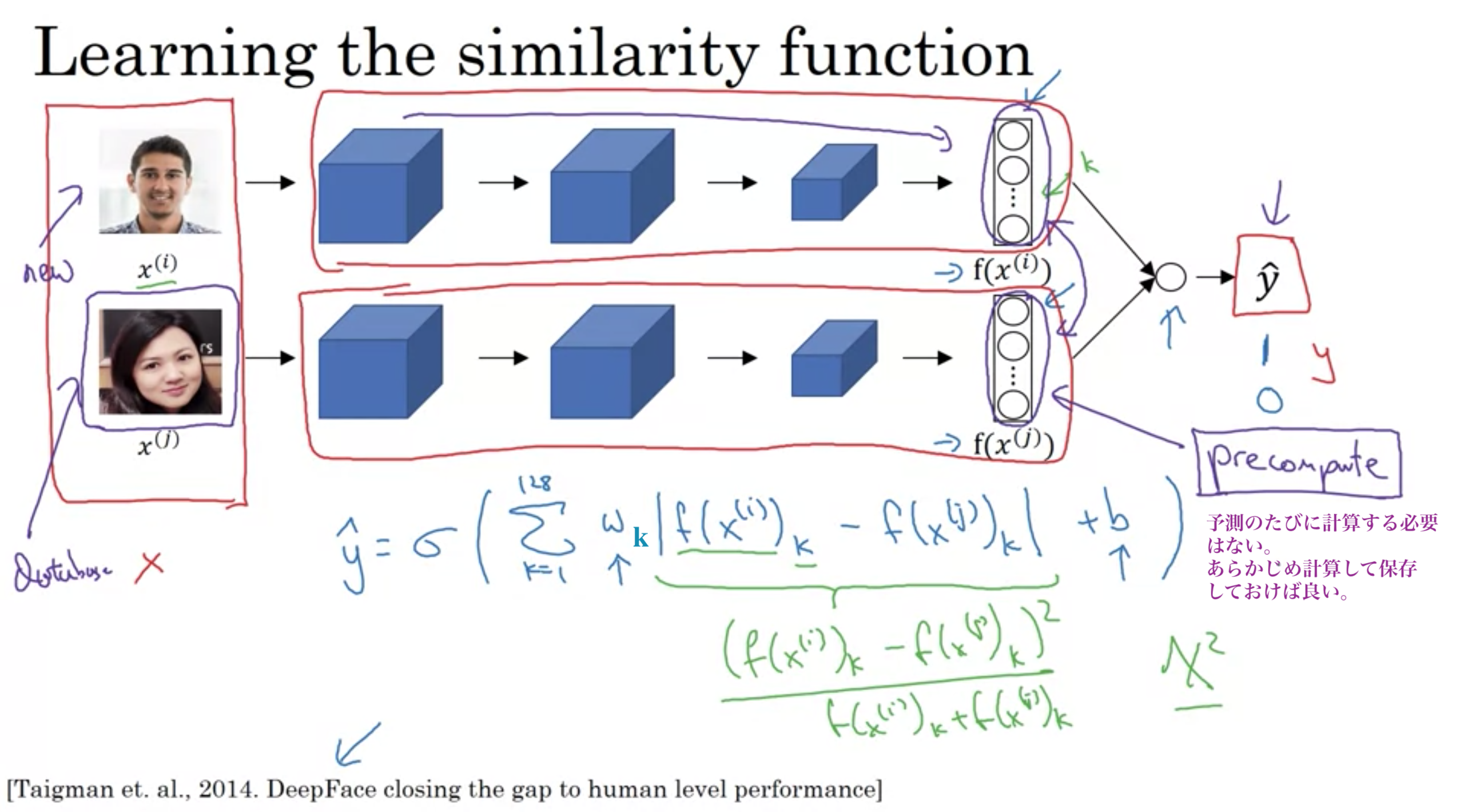


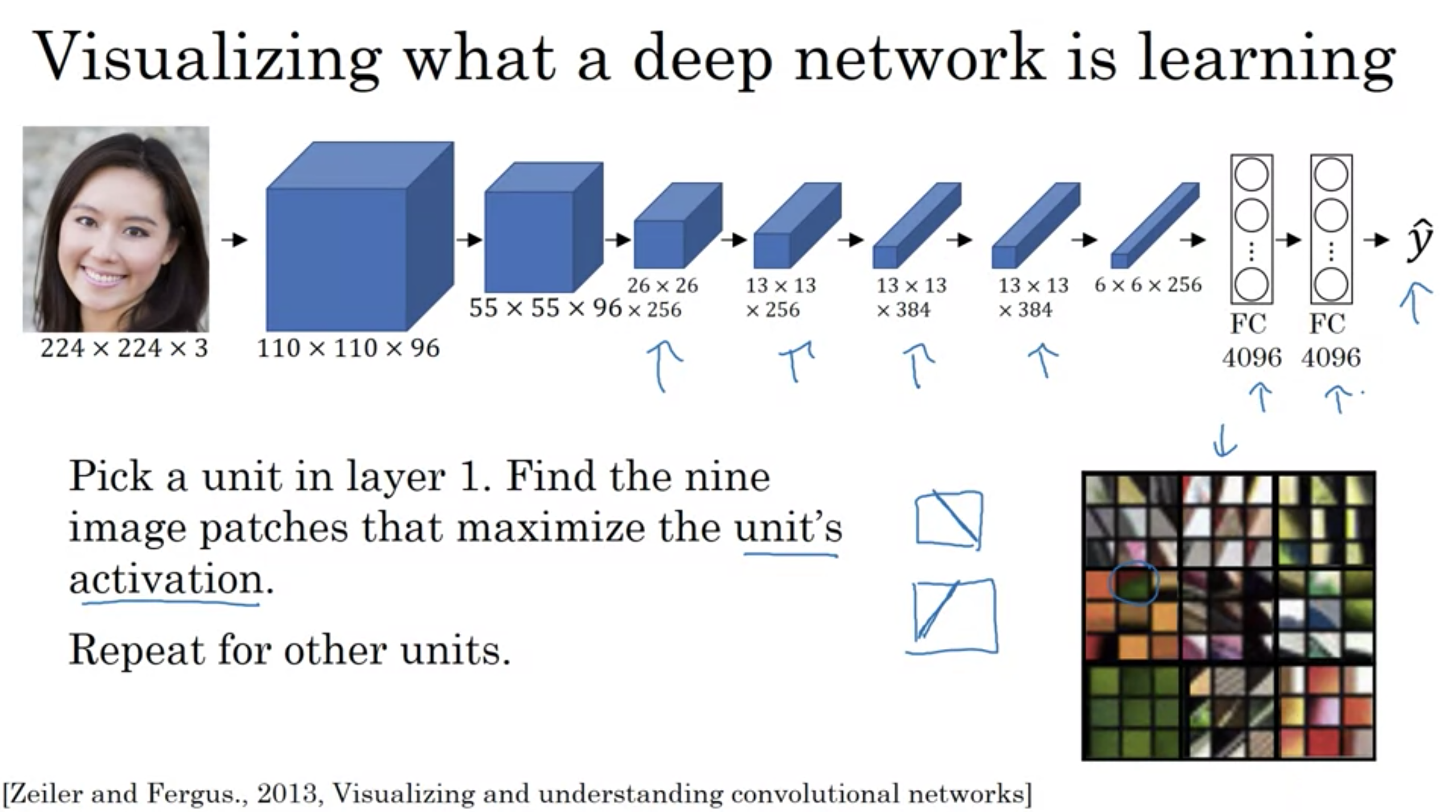 真相ネットワークが学習しているものの可視化
真相ネットワークが学習しているものの可視化
[論文] Visualizing and Understanding Convolutional Networks
 深層ネットワークの可視化 1層目
深層ネットワークの可視化 1層目
 深層ネットワークの可視化 2層目
深層ネットワークの可視化 2層目
 深層ネットワークの可視化 3層目
深層ネットワークの可視化 3層目 深層ネットワークの可視化 4層目
深層ネットワークの可視化 4層目
 深層ネットワークの可視化 5層目
深層ネットワークの可視化 5層目
層一でエッジを活性化、層二で複雑な形やパターンを検出、層三で人や車も検出できている、層四ではより高レベルな検出が、層五ではさらに複雑な検出がなされている
画風変換のコスト: \(J(G)=αJ _{ content }(C, G)+βJ _{ style }(S, G)\)
生成画像(Generated image)と正解画像の内容(Content)のコスト、生成画像と正解画像のスタイル(Style)のコストの和をとる
αとβは内容コストとスタイルコストで相対的な重みを指定する
 画風変換のコスト関数
画風変換のコスト関数
[論文] [Leon A. Gatys, 2015] A Neural Algorithm of Artistic Style
Gは生成画像のピクセル値

L2ノルム(各次元の値を2乗した和の平方根)の二乗
\(J _{ content }(C, G) = \frac{ 1 }{ 2 }|| a ^{ [l](C) }-a ^{ [l](G) } ||^2 \)
 Content cost function
Content cost function
全成分の二乗和のルートをフロベニウスノルム(行列の右下にFをかく)
例えば、行列Aのフロベニウスノルム \(‖A‖_F= \sqrt{ \sum_{ij} a^2_{ij} } \)
\( G_{kk'}^{[l](S)}=\textstyle \sum_{i=1}^{n _h} \textstyle \sum_{j=1}^ {n _w} a_{i,j,k}^{[l](S)} a_{i,j,k'}^{[l](S)} \)
\( G_{kk'}^{[l](G)}=\textstyle \sum_{i=1}^{n _h} \textstyle \sum_{j=1}^ {n _w} a_{i,j,k}^{[l](G)} a_{i,j,k'}^{[l](G)} \)
\( J_{style}^{[l]} (S, G)= \dfrac{ 1 }{ (2n^{[l]}_H n^{[l]}_W n^{[l]}_C)^2 } \textstyle \sum_k \sum_{k'} (G_{kk'}^{[l](S)}-G_{kk'}^{[l](G)})^2 \)


 Style cost function
Style cost function
1次元のデータにもConvNetを使用できる (実際にはRecurrent Neural Networkを使う)
・EKG信号心電図
・海抜高度
など
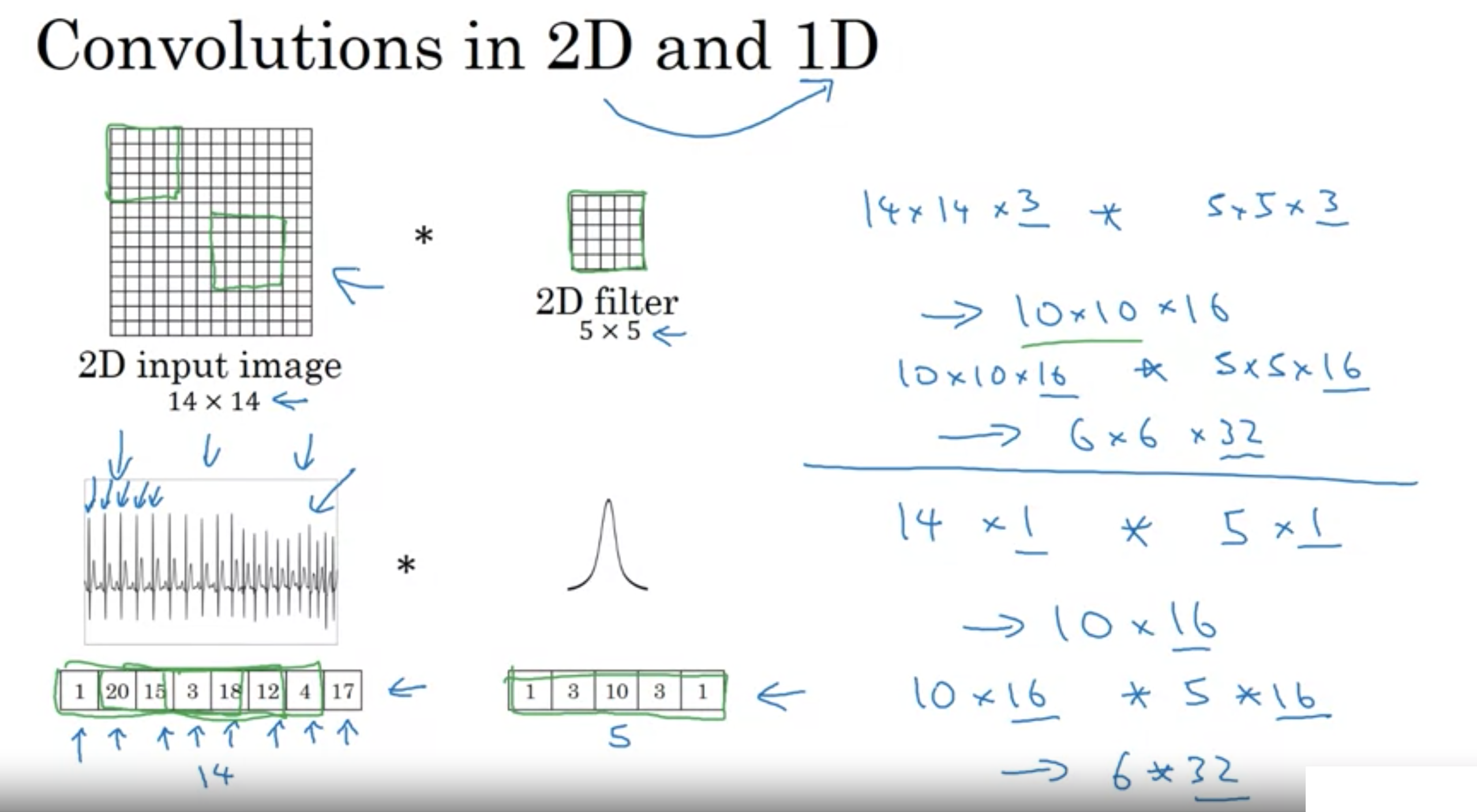 一次元と二次元の畳み込み
一次元と二次元の畳み込み
・X線によるCTスキャン (体の奥行きの断面)
・映画データ (映画の時間が異なる断面 映画内の人の動きを検出)
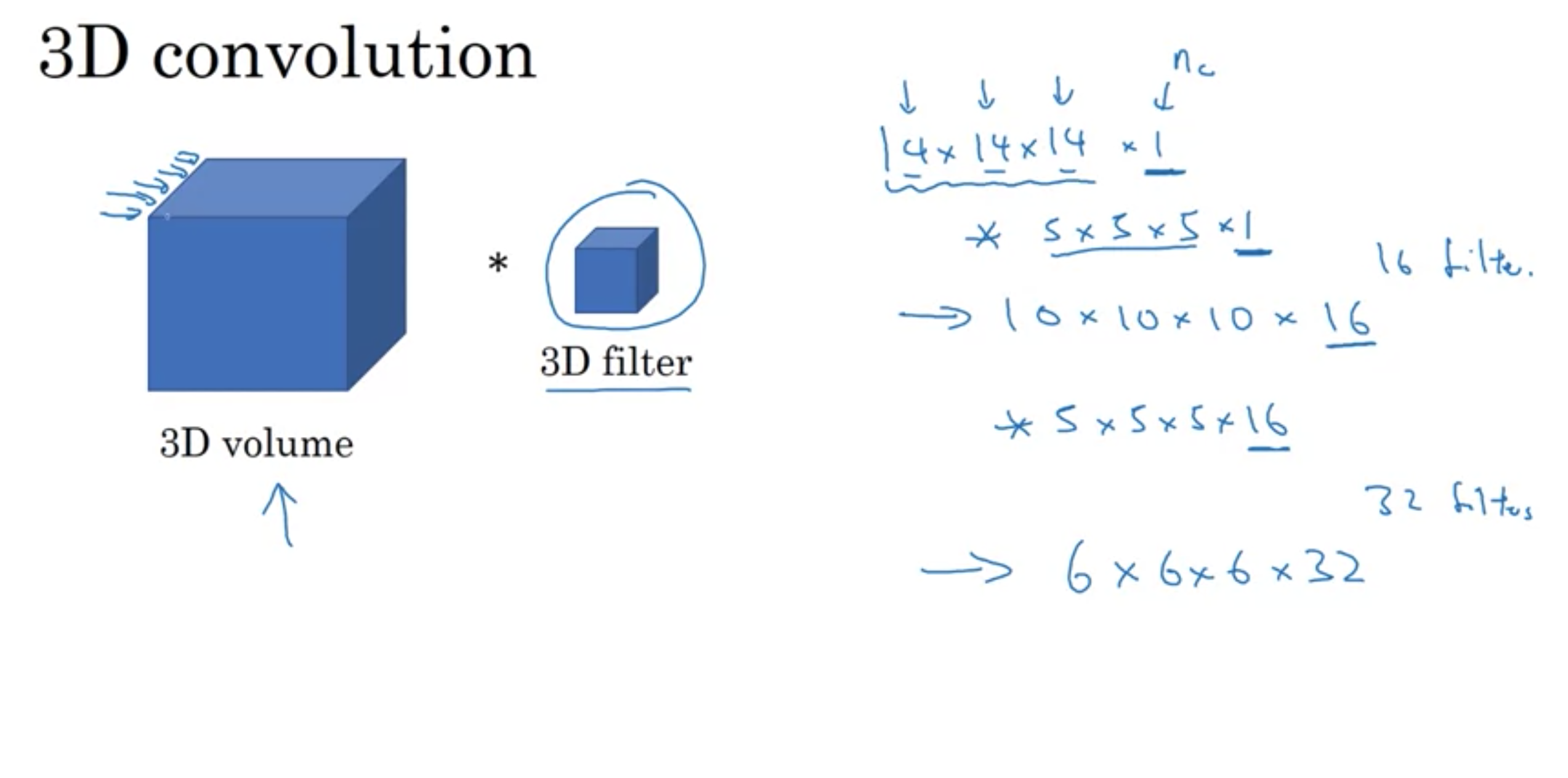
体全体に渡って、断面図を何重も重ね合わせた構造をとる、つまりデータは根本的に3次元 (高さ×幅×深さ×カラーチャンネル数)
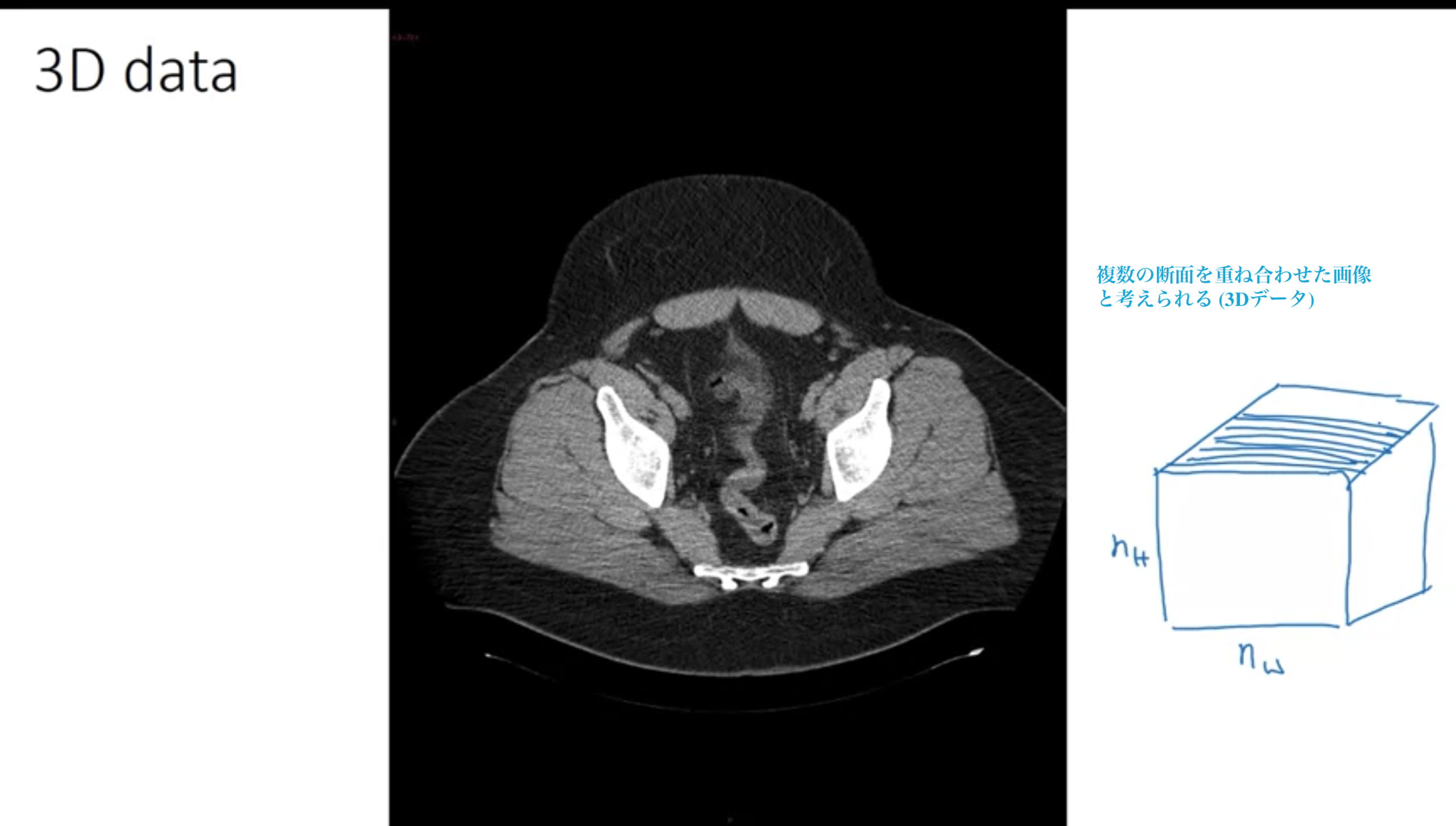 X線によるCTスキャン
X線によるCTスキャン
今回の講座はこちら!!
https://www.coursera.org/learn/convolutional-neural-networks/
CNNの理論から、論文での最近の実装やプログラミング演習など、書籍で学習するよりもはるかにわかりやすくまとまって最高の教材だと感じました。
初心者でもついていけるように一個一個きちんと理論から入っているので、初心者から中級者以上までお勧めできます。
ここまで綺麗に多くの情報がまとまった学習コンテンツは他にないと思うので、ぜひ学習にこのコースを利用することをお勧めします。
ちなみに筆者は今までいくつか深層学習の書籍を使って勉強してきましたが、間違いなく一番わかりやすくて多くの情報が学習できました。